Page 170 -

3.6 Geometric transformations 149

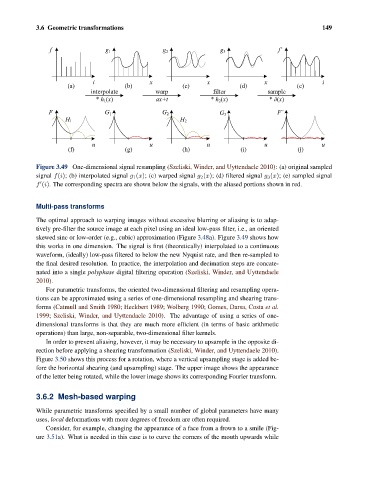
f g 1 g 2 g 3 f’

i x x x i
(a) (b) (c) (d) (e)
interpolate warp filter sample
* h 1(x) ax+t * h 2(x) * į(x)

F G 1 G 2 G 3 F’
H 1 H 2

u u u u u
(f) (g) (h) (i) (j)

Figure 3.49 One-dimensional signal resampling (Szeliski, Winder, and Uyttendaele 2010): (a) original sampled
signal f(i); (b) interpolated signal g 1 (x); (c) warped signal g 2 (x); (d) filtered signal g 3 (x); (e) sampled signal

f (i). The corresponding spectra are shown below the signals, with the aliased portions shown in red.

Multi-pass transforms

The optimal approach to warping images without excessive blurring or aliasing is to adap-
tively pre-filter the source image at each pixel using an ideal low-pass filter, i.e., an oriented
skewed sinc or low-order (e.g., cubic) approximation (Figure 3.48a). Figure 3.49 shows how
this works in one dimension. The signal is first (theoretically) interpolated to a continuous
waveform, (ideally) low-pass filtered to below the new Nyquist rate, and then re-sampled to
the final desired resolution. In practice, the interpolation and decimation steps are concate-
nated into a single polyphase digital filtering operation (Szeliski, Winder, and Uyttendaele
2010).
For parametric transforms, the oriented two-dimensional filtering and resampling opera-
tions can be approximated using a series of one-dimensional resampling and shearing trans-
forms (Catmull and Smith 1980; Heckbert 1989; Wolberg 1990; Gomes, Darsa, Costa et al.
1999; Szeliski, Winder, and Uyttendaele 2010). The advantage of using a series of one-
dimensional transforms is that they are much more efficient (in terms of basic arithmetic
operations) than large, non-separable, two-dimensional filter kernels.
In order to prevent aliasing, however, it may be necessary to upsample in the opposite di-
rection before applying a shearing transformation (Szeliski, Winder, and Uyttendaele 2010).
Figure 3.50 shows this process for a rotation, where a vertical upsampling stage is added be-
fore the horizontal shearing (and upsampling) stage. The upper image shows the appearance
of the letter being rotated, while the lower image shows its corresponding Fourier transform.

3.6.2 Mesh-based warping

While parametric transforms specified by a small number of global parameters have many
uses, local deformations with more degrees of freedom are often required.
Consider, for example, changing the appearance of a face from a frown to a smile (Fig-
ure 3.51a). What is needed in this case is to curve the corners of the mouth upwards while