Page 214 -

4.1 Points and patches 193

. . .

Scale
(next
octave)

Scale
(first
octave) Scale

Difference of
Gaussian Gaussian (DOG)
(a) (b)

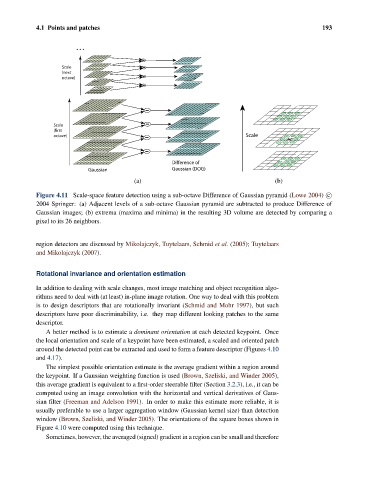
Figure 4.11 Scale-space feature detection using a sub-octave Difference of Gaussian pyramid (Lowe 2004) c
2004 Springer: (a) Adjacent levels of a sub-octave Gaussian pyramid are subtracted to produce Difference of
Gaussian images; (b) extrema (maxima and minima) in the resulting 3D volume are detected by comparing a
pixel to its 26 neighbors.

region detectors are discussed by Mikolajczyk, Tuytelaars, Schmid et al. (2005); Tuytelaars
and Mikolajczyk (2007).

Rotational invariance and orientation estimation
In addition to dealing with scale changes, most image matching and object recognition algo-
rithms need to deal with (at least) in-plane image rotation. One way to deal with this problem
is to design descriptors that are rotationally invariant (Schmid and Mohr 1997), but such
descriptors have poor discriminability, i.e. they map different looking patches to the same
descriptor.
A better method is to estimate a dominant orientation at each detected keypoint. Once
the local orientation and scale of a keypoint have been estimated, a scaled and oriented patch
around the detected point can be extracted and used to form a feature descriptor (Figures 4.10
and 4.17).
The simplest possible orientation estimate is the average gradient within a region around
the keypoint. If a Gaussian weighting function is used (Brown, Szeliski, and Winder 2005),
this average gradient is equivalent to a first-order steerable filter (Section 3.2.3), i.e., it can be
computed using an image convolution with the horizontal and vertical derivatives of Gaus-
sian filter (Freeman and Adelson 1991). In order to make this estimate more reliable, it is
usually preferable to use a larger aggregation window (Gaussian kernel size) than detection
window (Brown, Szeliski, and Winder 2005). The orientations of the square boxes shown in
Figure 4.10 were computed using this technique.
Sometimes, however, the averaged (signed) gradient in a region can be small and therefore