Page 238 -

4.2 Edges 217

W
SW 6 7
5 NW
N 0
NE
1
N 0

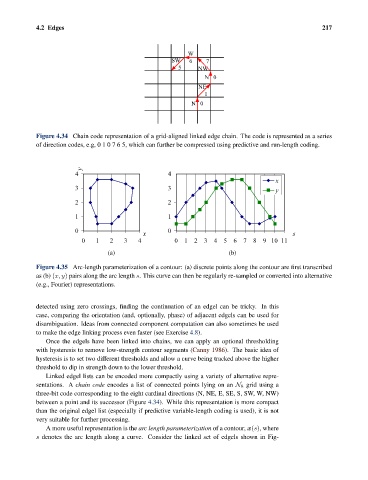
Figure 4.34 Chain code representation of a grid-aligned linked edge chain. The code is represented as a series
of direction codes, e.g,010765, which can further be compressed using predictive and run-length coding.

y .
4 4
x
3 3 y

2 2

1 1

0 0
x s
0 1 2 3 4 01 23 45 67 89 10 11
(a) (b)
Figure 4.35 Arc-length parameterization of a contour: (a) discrete points along the contour are first transcribed
as (b) (x, y) pairs along the arc length s. This curve can then be regularly re-sampled or converted into alternative
(e.g., Fourier) representations.

detected using zero crossings, finding the continuation of an edgel can be tricky. In this
case, comparing the orientation (and, optionally, phase) of adjacent edgels can be used for
disambiguation. Ideas from connected component computation can also sometimes be used
to make the edge linking process even faster (see Exercise 4.8).
Once the edgels have been linked into chains, we can apply an optional thresholding
with hysteresis to remove low-strength contour segments (Canny 1986). The basic idea of
hysteresis is to set two different thresholds and allow a curve being tracked above the higher
threshold to dip in strength down to the lower threshold.
Linked edgel lists can be encoded more compactly using a variety of alternative repre-
sentations. A chain code encodes a list of connected points lying on an N 8 grid using a
three-bit code corresponding to the eight cardinal directions (N, NE, E, SE, S, SW, W, NW)
between a point and its successor (Figure 4.34). While this representation is more compact
than the original edgel list (especially if predictive variable-length coding is used), it is not
very suitable for further processing.
A more useful representation is the arc length parameterization of a contour, x(s), where
s denotes the arc length along a curve. Consider the linked set of edgels shown in Fig-