Page 548 - Design for Six Sigma a Roadmap for Product Development

Design Optimization:Taguchi’s Robust Parameter Design 507

we can get the following relationships by Taylor series approximation:

Δg Δg Δg
y x 1 x 2 ... x n
Δx 1 Δx 2 Δx n
Δg Δg Δg
z 1 z 2 ... z m (14.9)
Δz 1 Δz 2 Δz m

and

∂g
∂g
∂g
Var(Y) y 2 x 1 2 x 2 ... 2 x n
2
2
2
2
∂x 1 ∂x 2 ∂x n

∂g
∂g
∂g
2 z 1 2 z 2 2 z m (14.10)

2
2
2
∂z 1 ∂z 2 ∂z m
From this equation, it is clear that we can reduce Var(Y) by
reducing either the sensitivities ∂g/∂x i , for i 1...n, which are the
sensitivities to the variation in design parameters, or ∂g/∂z j , for j
1...m, which are sensitivities to noise factors. Fortunately, many of
these sensitivities are influenced by the nominal values of design
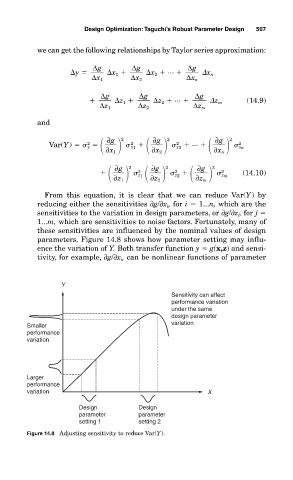
parameters. Figure 14.8 shows how parameter setting may influ-
ence the variation of Y. Both transfer function y g(x,z) and sensi-
tivity, for example, ∂g/∂x i , can be nonlinear functions of parameter
Y
Sensitivity can affect
performance variation
under the same
design parameter
Smaller variation
performance
variation
Larger
performance
variation X

Design Design
parameter parameter
setting 1 setting 2
Figure 14.8 Adjusting sensitivity to reduce Var(Y).