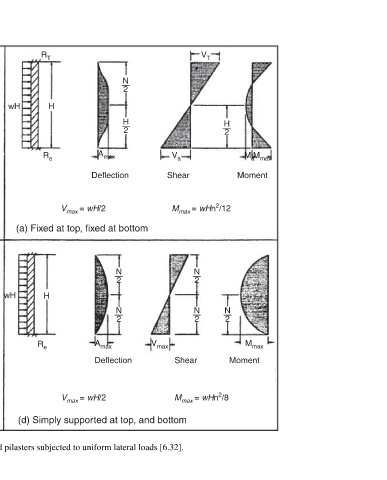
Page 426 - Design of Reinforced Masonry Structures

M a M max Moment M max Moment

H 2 N 2
V T M max = wHn 2 /12 N 2 N 2 M max = wHn 2 /8
Shear Shear
V a
V max

N 2 H 2 N 2 N 2
A max Deflection A max Deflection (d) Simply supported at top, and bottom
V max = wH/2 (a) Fixed at top, fixed at bottom V max = wH/2

H
R T R e H R e
wH wH

M max Moment M max Moment Formulas for maximum moments and shears for walls and pilasters subjected to uniform lateral loads [6.32].

M max = wHn 2 /2 1 H 4 M max = wH 2 /8

V max Shear V e Shear
V T H
5 8

Deflection Deflection
Δ max Δ max (c) Simply supported at top, fixed at bottom
V max = wH (a) Free at top, fixed at bottom V max = 5wH/8

H R e R T H R e FIGURE 6.43

wH wH

6.76