Page 263 - Distillation theory

P1: JPJ/FFX P2: JMT/FFX QC: FCH/FFX T1: FCH
0521820928c07 CB644-Petlyuk-v1 June 11, 2004 20:18

7.3 Design Calculation of Two-Section Columns 237

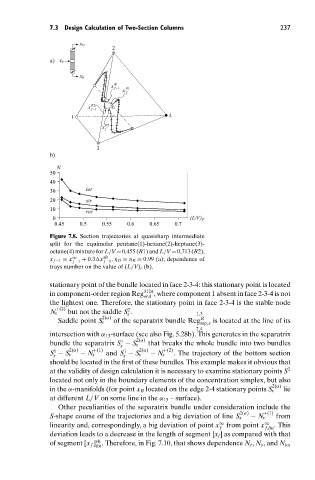
x D
2
a) x F

x B
x R f − 1
1
x R f 1
x R f − 2 1
1 4
x R 2
f

3
b)
N
50
40
30 tot
20 str
10 rec
0 (L/V) r
0.45 0.5 0.55 0.6 0.65 0.7

Figure 7.8. Section trajectories at quasisharp intermediate
split for the equimolar pentane(1)-hexane(2)-heptane(3)-
octane(4) mixture for L/V = 0.455 (R1) and L/V = 0.713 (R2),
x f −1 = x ∞ + 0.3 x sh ,η D = η B = 0.99 (a); dependence of
f −1
f −1
trays number on the value of (L/V) r (b).
stationary point of the bundle located in face 2-3-4: this stationary point is located
in component-order region Reg 3124 , where component 1 absent in face 2-3-4 is not
ord
the lightest one. Therefore, the stationary point in face 2-3-4 is the stable node
+(2) 2
N s but not the saddle S . 1,3
s
2(α) R
Saddle point S s of the separatrix bundle Reg sep,s is located at the line of its
2,4
intersection with α 13 -surface (see also Fig. 5.28b). This generates in the separatrix
1 2(α)
bundle the separatrix S − S s that breaks the whole bundle into two bundles
s
1 2(α) +(1) 1 2(α) +(2)
S − S s − N s and S − S s − N s . The trajectory of the bottom section
s s
should be located in the first of these bundles. This example makes it obvious that
at the validity of design calculation it is necessary to examine stationary points S 2
located not only in the boundary elements of the concentration simplex, but also
2(α)
in the α-manifolds (for point x B located on the edge 2-4 stationary points S s lie
at different L/V on some line in the α 13 – surface).
Other peculiarities of the separatrix bundle under consideration include the
2(α) +(1)
S-shape course of the trajectories and a big deviation of line S s − N s from
linearity and, correspondingly, a big deviation of point x ∞ from point x ∞ . This
f f,lin
deviation leads to a decrease in the length of segment [x f ] as compared with that
sh
of segment [x f ] . Therefore, in Fig. 7.10, that shows dependence N r , N s , and N tot
lin