Page 30 - Distillation theory

P1: FCH
0521820928c01 CB644-Petlyuk-v1 June 11, 2004 17:45

4 Phase Equilibrium and Its Geometric Presentation

yx
-

Az Az
-
T x-y

K 1 K 1 K 1 K 1 K 2
-
Kx
K 2 K 2 K 1
K 2 K 2
a) b) c) d)

yx
-

Az Az 1 Az 2 x L1 Az x L2 x L1 x L2 Az

-
T x-y

Az Az 1 Az 2 x L1 Az x L2 x L1 x L2 Az
K 1 K 2 K 1 K 1 K 2 K 1 K 2
K 1
K 1
-
Kx
K 2 K 2 K 2 K 1 K 2 K 2 K 1
K 2 K 1
Az Az 1 Az 2 x L1 Az x L2 x L1 x L2 Az
e) f) g) h)
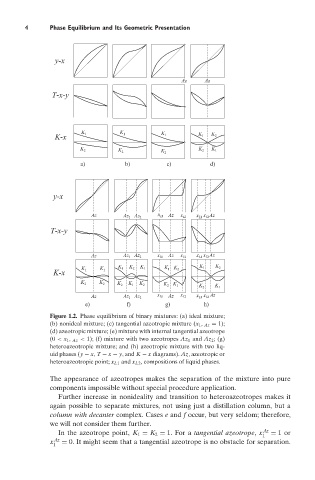
Figure 1.2. Phase equilibrium of binary mixtures: (a) ideal mixture;
(b) nonideal mixture; (c) tangential azeotropic mixture (x 1 , Az = 1);
(d) azeotropic mixture; (e) mixture with internal tangential azeotrope
(0 < x 1 , Az < 1); (f) mixture with two azeotropes Az 1 and Az 2 ; (g)
heteroazeotropic mixture; and (h) azeotropic mixture with two liq-
uid phases (y − x, T − x − y, and K − x diagrams). Az, azeotropic or
heteroazeotropic point; x L1 and x L2 , compositions of liquid phases.

The appearance of azeotropes makes the separation of the mixture into pure
components impossible without special procedure application.
Further increase in nonideality and transition to heteroazeotropes makes it
again possible to separate mixtures, not using just a distillation column, but a
column with decanter complex. Cases e and f occur, but very seldom; therefore,
we will not consider them further.
In the azeotrope point, K 1 = K 2 = 1. For a tangential azeotrope, x Az = 1or
1
x Az = 0. It might seem that a tangential azeotrope is no obstacle for separation.
1