Page 257 - Distributed model predictive control for plant-wide systems

Networked Distributed Predictive Control with Inputs and Information Structure Constraints 231

Table 10.2 Parameters of the N-DMPC
Subsystem K i P i Q i R i Δu max u max
i
i
Δu min u min
i i
S 1 −0.35 5.36 4 0.2 ±1 ±2
S 2 −0.25 5.35 4 0.2 ±1 ±2
S 3 −0.28 5.36 4 0.2 ±1 ±2
S 4 −0.43 5.38 4 0.2 ±1 ±2

x 1
1
x 2
x 3
x 4
0.5
x i

0

–0.5
5 10 15 20
Time (s)

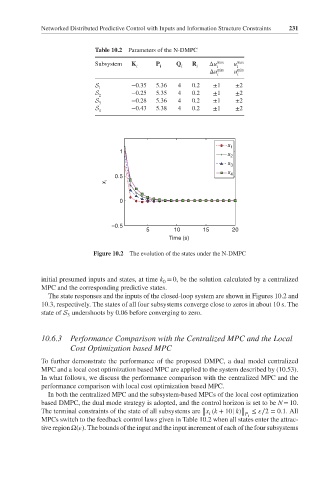
Figure 10.2 The evolution of the states under the N-DMPC

initial presumed inputs and states, at time k = 0, be the solution calculated by a centralized
0
MPC and the corresponding predictive states.
The state responses and the inputs of the closed-loop system are shown in Figures 10.2 and
10.3, respectively. The states of all four subsystems converge close to zeros in about 10 s. The
state of S undershoots by 0.06 before converging to zero.
3

10.6.3 Performance Comparison with the Centralized MPC and the Local
Cost Optimization based MPC
To further demonstrate the performance of the proposed DMPC, a dual model centralized
MPC and a local cost optimization based MPC are applied to the system described by (10.53).
In what follows, we discuss the performance comparison with the centralized MPC and the
performance comparison with local cost optimization based MPC.
In both the centralized MPC and the subsystem-based MPCs of the local cost optimization
based DMPC, the dual mode strategy is adopted, and the control horizon is set to be N = 10.
The terminal constraints of the state of all subsystems are x (k + 10|k) ‖ ≤ ∕2 = 0.1. All
‖
‖ i
‖P i
MPCs switch to the feedback control laws given in Table 10.2 when all states enter the attrac-
tive region Ω( ). The bounds of the input and the input increment of each of the four subsystems