Page 85 - Distributed model predictive control for plant-wide systems

Structure Model and System Decomposition 59

4.4.1 RGA Definition

We follow [86] here and show that the RGA provides a measure of interactions. Let u and
j
y denote a particular manipulated variable-controlled variable pair for the MIMO plant G(s),
i
and assume that our task is to use u to control y .
i
j
In general, the process gain y / u can be evaluated in two extreme cases [86]:
j
i
• Other loop is open
( )
y i
= g ij (4.24)
u
j u k =0,k≠j
• Other loop is closed
( )
y
i
= ̂g ij (4.25)
u j y k =0,k≠j
where g = Element(G, i, j)isthe ith row and jth column element of G, whereas
ij
ˆ g = 1/Element(G − 1 , j, i)isthe inverseofthe jth row and ith column element of G − 1 .
ij
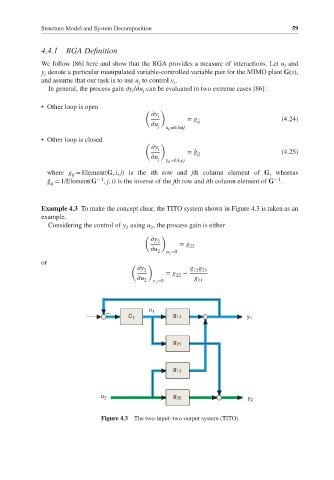
Example 4.3 To make the concept clear, the TITO system shown in Figure 4.3 is taken as an
example.
Considering the control of y using u , the process gain is either
2 2
( )
y 2
= g 22
u
2 u 1 =0
or ( )
y 2 g g
12 21
= g −
22
u 2 y 1 =0 g 11

– u 1
C 1 g 11 y 1

g 21

g 12

u 2 g 22
y 2

Figure 4.3 The two-input–two-output system (TITO)