Page 245 - Dust Explosions in the Process Industries

Generation of Explosible Dust Clouds 217

lV3 lU2 lb-' 1 10 102 103
Relative velocity, v,, , between particle and air h/Sl

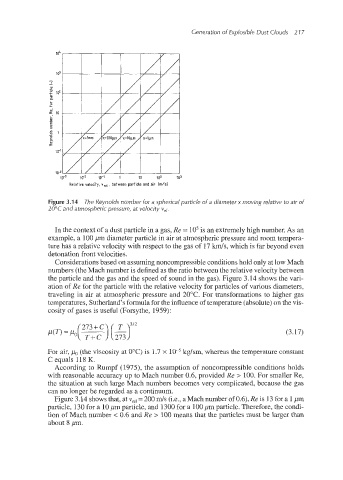
Figure 3.34 The Reynolds number for a spherical particle of a diameter x moving relative to air of
20°C and atmospheric pressure, at velocity vel.

In the context of a dust particle in a gas, Re = lo5is an extremely high number. As an
example, a 100 pm diameter particle in air at atmosphericpressure and room tempera-
ture has a relative velocity with respect to the gas of 17 Ws, which is far beyond even
detonation front velocities.
Considerations based on assuming noncompressible conditions hold only at low Mach
numbers (the Mach number is defined as the ratio between the relative velocity between
the particle and the gas and the speed of sound in the gas). Figure 3.14 shows the vari-
ation of Re for the particle with the relative velocity for particles of various diameters,
traveling in air at atmospheric pressure and 20°C. For transformations to higher gas
temperatures,Sutherland's formula for the influence of temperature (absolute) on the vis-
cosity of gases is useful (Forsythe, 1959):

(3.17)

For ais, p, (the viscosity at 0OC) is 1.7 x kg/sm, whereas the temperature constant
C equals 118 K.
According to Rumpf (1975), the assumption of noncompressible conditions holds
with reasonable accuracy up to Mach number 0.6, provided Re > 100. For smaller Re,
the situation at such large Mach numbers becomes very complicated, because the gas
can no longer be regarded as a continuum.
Figure 3.14 shows that, at qel=200 m/s (i.e., a Mach number of 0.6),Re is 13for a 1,urn
particle, 130 for a 10pm particle, and 1300 for a 100pm particle. Therefore, the condi-
tion of Mach number < 0.6 and Re > 100 means that the particles must be larger than
about 8 prn.