Page 248 - Dust Explosions in the Process Industries

220 Dust Explosions in the Process Industries

where a is the sound speed in the particle free gas, @ is the mass fraction of particles in
the dust cloud, 6is the ratio between the specificheat of the particle material and the spe-
cific heat at a constant pressure of the gas, and y is the specific heat ratio CJC, for the
gas. Values for the specificheat of various solids as a function of temperature, partly based
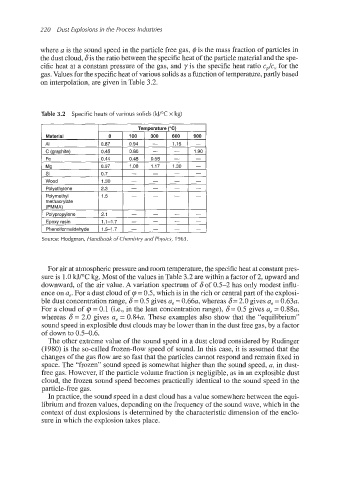
on interpolation, are given in Table 3.2.

Table 3.2 Specific heats of various solids (kJ/”C x kg)

Source: Hodgman, Handbook of Chemistry and Physics, 1963.

For air at atmosphericpressure and room temperature, the specificheat at constantpres-
sure is 1.O U/”C kg. Most of the values in Table 3.2 are within a factor of 2, upward and
downward, of the air value. A variation spectrum of 6 of 0.5-2 has only modest influ-
ence on a,. For a dust cloud of q =0.5, which is in the rich or centralpart of the explosi-
ble dust concentrationrange, 6=0.5 gives a, = 0.66a, whereas 6= 2.0 gives a, = 0.63a.
For a cloud of q = 0.1 (i.e., in the lean concentration range), 6= 0.5 gives a, = 0.88a,
whereas 6 = 2.0 gives a, = 0.84a. These examples also show that the “equilibrium”
sound speed in explosibledust clouds may be lower than in the dust free gas, by a factor
of down to 0.5-0.6.
The other extreme value of the sound speed in a dust cloud considered by Rudinger
(1980) is the so-called frozen-flow speed of sound. In this case, it is assumed that the
changes of the gas flow are so fast that the particles cannot respond and remain fixed in
space. The “frozen” sound speed is somewhat higher than the sound speed, a, in dust-
free gas. However, if the particle volume fraction is negligible, as in an explosible dust
cloud, the frozen sound speed becomes practically identical to the sound speed in the
particle-free gas.
In practice, the sound speed in a dust cloud has a value somewhere between the equi-
librium and frozen values, depending on the frequency of the sound wave, which in the
context of dust explosions is determined by the characteristic dimension of the enclo-
sure in which the explosion takes place.