Page 126 - Dynamic Loading and Design of Structures

Page 103

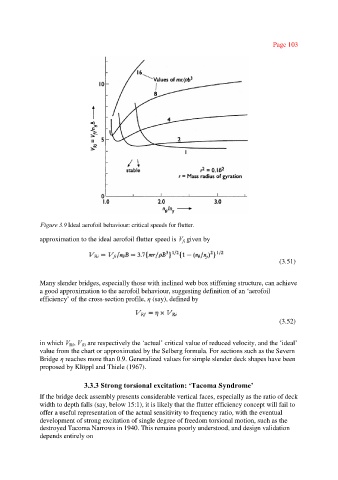
Figure 3.9 Ideal aerofoil behaviour: critical speeds for flutter.

approximation to the ideal aerofoil flutter speed is V given by
fi

(3.51)

Many slender bridges, especially those with inclined web box stiffening structure, can achieve
a good approximation to the aerofoil behaviour, suggesting definition of an ‘aerofoil
efficiency’ of the cross-section profile, η(say), defined by

(3.52)

in which V , V are respectively the ‘actual’ critical value of reduced velocity, and the ‘ideal’
Rf
Ri
value from the chart or approximated by the Selberg formula. For sections such as the Severn
Bridge ηreaches more than 0.9. Generalized values for simple slender deck shapes have been
proposed by Klöppl and Thiele (1967).

3.3.3 Strong torsional excitation: ‘Tacoma Syndrome’
If the bridge deck assembly presents considerable vertical faces, especially as the ratio of deck
width to depth falls (say, below 15:1), it is likely that the flutter efficiency concept will fail to
offer a useful representation of the actual sensitivity to frequency ratio, with the eventual
development of strong excitation of single degree of freedom torsional motion, such as the
destroyed Tacoma Narrows in 1940. This remains poorly understood, and design validation
depends entirely on