Page 125 - Dynamic Loading and Design of Structures

Page 102

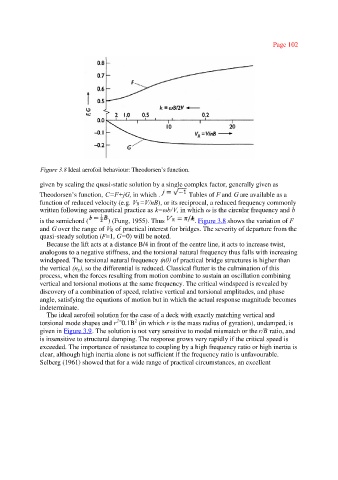
Figure 3.8 Ideal aerofoil behaviour: Theodorsen’s function.

given by scaling the quasi-static solution by a single complex factor, generally given as
Theodorsen’s function, C=F+jG, in which . Tables of F and G are available as a
function of reduced velocity (e.g. VR=V/nB), or its reciprocal, a reduced frequency commonly
written following aeronautical practice as k=ωb/V, in which ωis the circular frequency and b

is the semichord ( ) (Fung, 1955). Thus . Figure 3.8 shows the variation of F
and G over the range of VR of practical interest for bridges. The severity of departure from the
quasi-steady solution (F=1, G=0) will be noted.
Because the lift acts at a distance B/4 in front of the centre line, it acts to increase twist,
analogous to a negative stiffness, and the torsional natural frequency thus falls with increasing
)
windspeed. The torsional natural frequency (nθof practical bridge structures is higher than
the vertical (ny), so the differential is reduced. Classical flutter is the culmination of this
process, when the forces resulting from motion combine to sustain an oscillation combining
vertical and torsional motions at the same frequency. The critical windspeed is revealed by
discovery of a combination of speed, relative vertical and torsional amplitudes, and phase
angle, satisfying the equations of motion but in which the actual response magnitude becomes
indeterminate.
The ideal aerofoil solution for the case of a deck with exactly matching vertical and
2=
2
torsional mode shapes and r 0.1B (in which r is the mass radius of gyration), undamped, is
given in Figure 3.9. The solution is not very sensitive to modal mismatch or the r/B ratio, and
is insensitive to structural damping. The response grows very rapidly if the critical speed is
exceeded. The importance of resistance to coupling by a high frequency ratio or high inertia is
clear, although high inertia alone is not sufficient if the frequency ratio is unfavourable.
Selberg (1961) showed that for a wide range of practical circumstances, an excellent