Page 246 - Dynamic Loading and Design of Structures

Page 217

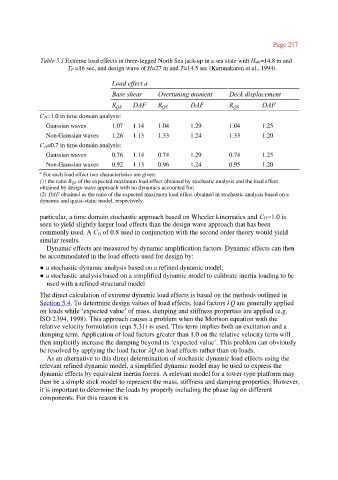
Table 5.1 Extreme load effects in three-legged North Sea jack-up in a sea state with Hm0=14.8 m and
TP =16 sec, and design wave of H=27 m and T=14.5 sec (Karunakaren et al., 1994).

Load effect a

Base shear Overtuning moment Deck displacement
R QS DAF R QS DAF R QS DAF

C D=1.0 in time domain analysis:
Gaussian waves 1.07 1.14 1.04 1.29 1.04 1.25
Non-Gaussian waves 1.26 1.13 1.33 1.24 1.33 1.20
C =0.7 in time domain analysis:
D
Gaussian waves 0.76 1.14 0.74 1.29 0.74 1.25
Non-Gaussian waves 0.92 1.13 0.96 1.24 0.95 1.20
a For each load effect two characteristics are given:
(1) the ratio R QS of the expected maximum load effect obtained by stochastic analysis and the load effect
obtained by design wave approach with no dynamics accounted for;
(2) DAF obtained as the ratio of the expected maximum load effect obtained in stochastic analysis based on a
dynamic and quasi-static model, respectively.

particular, a time domain stochastic approach based on Wheeler kinematics and CD=1.0 is
seen to yield slightly larger load effects than the design wave approach that has been
commonly used. A C of 0.8 used in conjunction with the second order theory would yield
D
similar results.
Dynamic effects are measured by dynamic amplification factors. Dynamic effects can then
be accommodated in the load effects used for design by:

●a stochastic dynamic analysis based on a refined dynamic model;
●a stochastic analysis based on a simplified dynamic model to calibrate inertia loading to be
used with a refined structural model

The direct calculation of extreme dynamic load effects is based on the methods outlined in
Section 5.4. To determine design values of load effects, load factors λQ are generally applied
on loads while ‘expected value’ of mass, damping and stiffness properties are applied (e.g.
ISO 2394, 1998). This approach causes a problem when the Morison equation with the
relative velocity formulation (eqn 5.31) is used. This term implies both an excitation and a
damping term. Application of load factors greater than 1.0 on the relative velocity term will
then implicitly increase the damping beyond its ‘expected value’. This problem can obviously
be resolved by applying the load factor λQ on load effects rather than on loads.
As an alternative to this direct determination of stochastic dynamic load effects using the
relevant refined dynamic model, a simplified dynamic model may be used to express the
dynamic effects by equivalent inertia forces. A relevant model for a tower-type platform may
then be a simple stick model to represent the mass, stiffness and damping properties. However,
it is important to determine the loads by properly including the phase lag on different
components. For this reason it is