Page 131 - Electrical Properties of Materials

The effective mass 113

as the effective mass of an electron. Thus, the answer to the original question
is that an electron in a crystal lattice does react to an electric field, but its mass
is given by eqn (7.42) in contrast to the mass of a free electron. Let us just
check whether we run into any contradiction with our E–k curve for a free
electron. Then
2 2
k
E = ,
2m
and thus

2
∂ E 2
= ,
∂k 2 m
which substituted into eqn (7.42) gives

m = m.
∗
E
So everything is all right.
For an electron in a one-dimensional lattice we may take E in the form of (a)
eqn (7.30), giving

2
∗
m = sec ka. (7.43)
2Aa 2
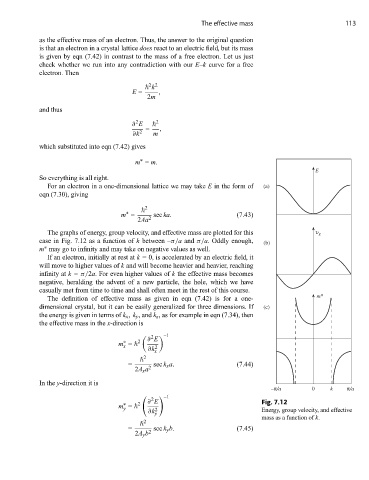
The graphs of energy, group velocity, and effective mass are plotted for this υ g
case in Fig. 7.12 as a function of k between –π/a and π/a. Oddly enough, (b)
m may go to infinity and may take on negative values as well.
∗
If an electron, initially at rest at k = 0, is accelerated by an electric field, it
will move to higher values of k and will become heavier and heavier, reaching
infinity at k = π/2a. For even higher values of k the effective mass becomes
negative, heralding the advent of a new particle, the hole, which we have
casually met from time to time and shall often meet in the rest of this course.
The definition of effective mass as given in eqn (7.42) is for a one- m*
dimensional crystal, but it can be easily generalized for three dimensions. If (c)
the energy is given in terms of k x , k y , and k z , as for example in eqn (7.34), then
the effective mass in the x-direction is

2
∂ E –1
∗
m = 2
x
∂k x 2
2
= sec k x a. (7.44)
2A x a 2
In the y-direction it is
–π/a 0 k π/a
–1
2
∂ E Fig. 7.12
2
∗
m =
y 2
∂k y Energy, group velocity, and effective
mass as a function of k.
2
= sec k y b. (7.45)
2A y b 2