Page 133 - Electrical Properties of Materials

The number of possible states per band 115

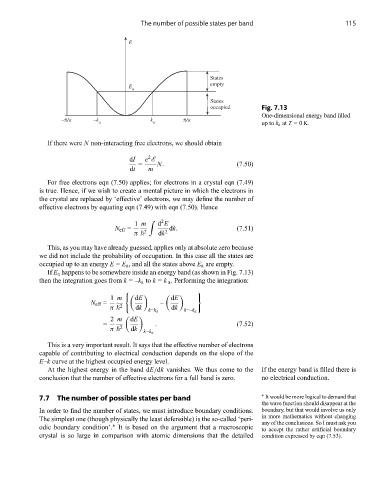
E

States
empty
E
a
States
occupied Fig. 7.13
One-dimensional energy band filled
–π/a –k k π/a
a a up to k a at T =0 K.

If there were N non-interacting free electrons, we should obtain
2
dI e E
= N. (7.50)
dt m
For free electrons eqn (7.50) applies; for electrons in a crystal eqn (7.49)
is true. Hence, if we wish to create a mental picture in which the electrons in
the crystal are replaced by ‘effective’ electrons, we may define the number of
effective electrons by equating eqn (7.49) with eqn (7.50). Hence

2
1 m d E
N eff = dk. (7.51)
π 2 dk 2
This, as you may have already guessed, applies only at absolute zero because
we did not include the probability of occupation. In this case all the states are
occupied up to an energy E = E a , and all the states above E a are empty.
If E a happens to be somewhere inside an energy band (as shown in Fig. 7.13)
then the integration goes from k =–k a to k = k a . Performing the integration:

1 m dE dE
N eff = –
π 2 dk dk
k=k a k=–k a
2 m dE
= . (7.52)
π 2 dk
k=k a
This is a very important result. It says that the effective number of electrons
capable of contributing to electrical conduction depends on the slope of the
E–k curve at the highest occupied energy level.
At the highest energy in the band dE/dk vanishes. We thus come to the If the energy band is filled there is
conclusion that the number of effective electrons for a full band is zero. no electrical conduction.

7.7 The number of possible states per band ∗ It would be more logical to demand that
the wave function should disappear at the
In order to find the number of states, we must introduce boundary conditions. boundary, but that would involve us only
The simplest one (though physically the least defensible) is the so-called ‘peri- in more mathematics without changing
any of the conclusions. So I must ask you
∗
odic boundary condition’. It is based on the argument that a macroscopic to accept the rather artificial boundary
crystal is so large in comparison with atomic dimensions that the detailed condition expressed by eqn (7.53).