Page 156 - Electrical Properties of Materials

138 Semiconductors

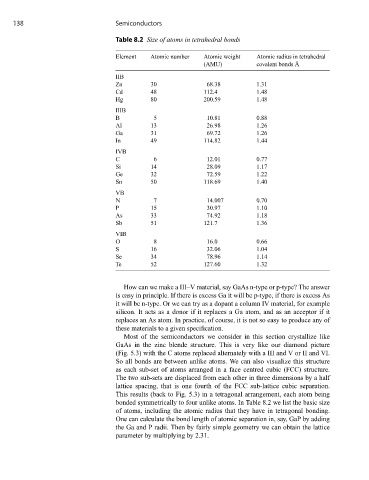
Table 8.2 Size of atoms in tetrahedral bonds

Element Atomic number Atomic weight Atomic radius in tetrahedral
(AMU) covalent bonds Å

IIB
Zn 30 68.38 1.31
Cd 48 112.4 1.48
Hg 80 200.59 1.48
IIIB
B 5 10.81 0.88
Al 13 26.98 1.26
Ga 31 69.72 1.26
In 49 114.82 1.44
IVB
C 6 12.01 0.77
Si 14 28.09 1.17
Ge 32 72.59 1.22
Sn 50 118.69 1.40
VB
N 7 14.007 0.70
P 15 30.97 1.10
As 33 74.92 1.18
Sb 51 121.7 1.36
VIB
O 8 16.0 0.66
S 16 32.06 1.04
Se 34 78.96 1.14
Te 52 127.60 1.32

How can we make a III–V material, say GaAs n-type or p-type? The answer
is easy in principle. If there is excess Ga it will be p-type, if there is excess As
it will be n-type. Or we can try as a dopant a column IV material, for example
silicon. It acts as a donor if it replaces a Ga atom, and as an acceptor if it
replaces an As atom. In practice, of course, it is not so easy to produce any of
these materials to a given specification.
Most of the semiconductors we consider in this section crystallize like
GaAs in the zinc blende structure. This is very like our diamond picture
(Fig. 5.3) with the C atoms replaced alternately with a III and V or II and VI.
So all bonds are between unlike atoms. We can also visualize this structure
as each sub-set of atoms arranged in a face centred cubic (FCC) structure.
The two sub-sets are displaced from each other in three dimensions by a half
lattice spacing, that is one fourth of the FCC sub-lattice cubic separation.
This results (back to Fig. 5.3) in a tetragonal arrangement, each atom being
bonded symmetrically to four unlike atoms. In Table 8.2 we list the basic size
of atoms, including the atomic radius that they have in tetragonal bonding.
One can calculate the bond length of atomic separation in, say, GaP by adding
the Ga and P radii. Then by fairly simple geometry we can obtain the lattice
parameter by multiplying by 2.31.