Page 22 - Elements of Distribution Theory

P1: JZP
052184472Xc01 CUNY148/Severini May 24, 2005 17:52

8 Properties of Probability Distributions

1.4 Distribution Functions

Consider a real-valued random variable X. The properties of X are described by its proba-
bility function P X , which gives the probability that X ∈ A for any set A ⊂ R.However,itis
also possible to specify the distribution of a random variable by considering Pr(X ∈ A) for a
limited class of sets A; this approach has the advantage that the function giving such proba-
bilitiesmaybeeasiertouseincomputations.Forinstance,considersetsoftheform(−∞, x],
for x ∈ R,so that P X {(−∞, x]} gives Pr(X ≤ x). The distribution function of the distribu-
tion of X or, simply, the distribution function of X,is the function F ≡ F X : R → [0, 1]
given by
F(x) = Pr(X ≤ x), −∞ < x < ∞.

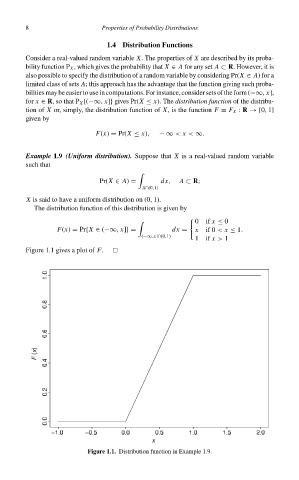
Example 1.9 (Uniform distribution). Suppose that X is a real-valued random variable
such that

Pr(X ∈ A) = dx, A ⊂ R;
A∩(0,1)
X is said to have a uniform distribution on (0, 1).
The distribution function of this distribution is given by
0 if x ≤ 0

F(x) = Pr{X ∈ (−∞, x]}= dx = x if 0 < x ≤ 1.
(−∞,x]∩(0,1)
1 if x > 1
Figure 1.1 gives a plot of F.

F (x)

− −
x
Figure 1.1. Distribution function in Example 1.9.