Page 200 - Academic Press Encyclopedia of Physical Science and Technology 3rd Organic Chemistry

P1: LLL/GVX P2: GQT Final Pages
Encyclopedia of Physical Science and Technology EN011G-539 July 14, 2001 21:48

Organic Chemical Systems, Theory 447

and higher electronic excited singlet states can be identi- through the nuclear configuration space. It is possible to
fied. Among the triplet wave functions the one with the visualize the vibrational motions of the molecule as well
lowest energy is called ψ(T 1 ) and its energy E(T 1 ). Simi- as its internal rotations as the motions of a marble rolling
larly, higher triplet state wave functions and their energies on the potential energy surface.
are identified. If the molecule is isolated, its total energy will remain
A different molecular geometry is then chosen and the constant and the marble will perform endless frictionless
process repeated. While this is difficult to do in practice, motion on the surface, trading the potential energy against
one can at least imagine performing this kind of opera- the kinetic energy of nuclear motion and vice versa. If the
tion for all possible molecular geometries. In a plot of molecule exchanges energy with its environment, it will
E(S 0 ) against the values of the geometrical parameters tend to lose any excess energy it may have and settle in
that describe the molecular structure, a surface will then one of the valleys or minima on the surface.
result. This is the potential energy surface for this particu- A proper description of the motion that corresponds
lar electronic state of the molecule (the potential energy of to vibrations and internal rotations again must be quan-
the molecule is its total energy minus the energy of overall tum mechanical since even the relatively heavy nuclei re-
translational, rotational, and vibrational motion). ally obey quantum rather than classical mechanics. Once
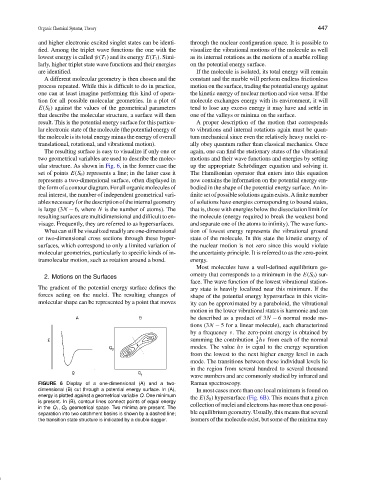
The resulting surface is easy to visualize if only one or again, one can find the stationary states of the vibrational
two geometrical variables are used to describe the molec- motions and their wave functions and energies by setting
ular structure. As shown in Fig. 6, in the former case the up the appropriate Schr¨odinger equation and solving it.
set of points E(S 0 ) represents a line; in the latter case it The Hamiltonian operator that enters into this equation
represents a two-dimensional surface, often displayed in now contains the information on the potential energy em-
the form of a contour diagram. For all organic molecules of bodied in the shape of the potential energy surface. An in-
real interest, the number of independent geometrical vari- finite set of possible solutions again exists. A finite number
ablesnecessaryforthedescriptionoftheinternalgeometry of solutions have energies corresponding to bound states,
is large (3N − 6, where N is the number of atoms). The that is, those with energies below the dissociation limit for
resulting surfaces are multidimensional and difficult to en- the molecule (energy required to break the weakest bond
visage. Frequently, they are referred to as hypersurfaces. and separate one of the atoms to infinity). The wave func-
What can still be visualized readily are one-dimensional tion of lowest energy represents the vibrational ground
or two-dimensional cross sections through these hyper- state of the molecule. In this state the kinetic energy of
surfaces, which correspond to only a limited variation of the nuclear motion is not zero since this would violate
molecular geometries, particularly to specific kinds of in- the uncertainty principle. It is referred to as the zero-point
tramolecular motion, such as rotation around a bond. energy.
Most molecules have a well-defined equilibrium ge-
ometry that corresponds to a minimum in the E(S 0 ) sur-
2. Motions on the Surfaces
face. The wave function of the lowest vibrational station-
The gradient of the potential energy surface defines the ary state is heavily localized near this minimum. If the
forces acting on the nuclei. The resulting changes of shape of the potential energy hypersurface in this vicin-
molecular shape can be represented by a point that moves ity can be approximated by a paraboloid, the vibrational
motion in the lower vibrational states is harmonic and can
be described as a product of 3N − 6 normal mode mo-
tions (3N − 5 for a linear molecule), each characterized
by a frequency ν. The zero-point energy is obtained by
1
summing the contribution hν from each of the normal
2
modes. The value hν is equal to the energy separation
from the lowest to the next higher energy level in each
mode. The transitions between these individual levels lie
in the region from several hundred to several thousand
wave numbers and are commonly studied by infrared and
FIGURE 6 Display of a one-dimensional (A) and a two- Raman spectroscopy.
dimensional (B) cut through a potential energy surface. In (A), In most cases more than one local minimum is found on
energy is plotted against a geometrical variable Q. One minimum the E(S 0 ) hypersurface (Fig. 6B). This means that a given
is present. In (B), contour lines connect points of equal energy
in the Q 1 , Q 2 geometrical space. Two minima are present. The collection of nuclei and electrons has more than one possi-
separation into two catchment basins is shown by a dashed line; ble equilibrium geometry. Usually, this means that several
the transition state structure is indicated by a double dagger. isomers of the molecule exist, but some of the minima may