Page 117 - Engineered Interfaces in Fiber Reinforced Composites

100 Engineered interfaces in jber reinforced composites

where PI is given in Eq. (4.3) and the Young’s modulus ratio of the composite to the
fiber, a2 = E,/Ef. When Young’s modulus of the composite, E,, is calculated based
on the simple rule of mixtures (i.e. E, = VfEf + (1 - C)E,,,), the stress distributions in
Rosen’s model are essentially identical to Cox’s model, regardless of the fiber
volume fraction, 6. This is because a variation in 6 influence to the same extent
both E, and the applied stress, 0,’ in Eqs (4.5) and (4.6) due to the assumption of
perfectly elastic and isotropic fiber and matrix.
The significance of Rosen’s work lies in the attempt of quantifying the efficiency
of stress transfer across the interface with respect to the fiber length, by introducing
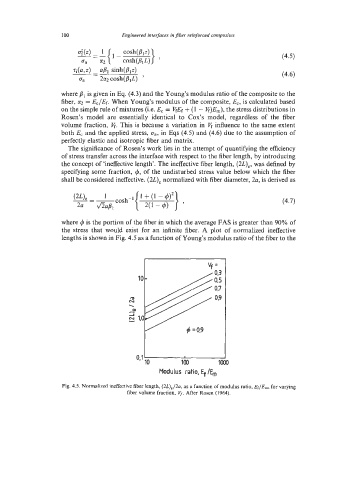
the concept of ‘ineffective length’. The ineffective fiber length, (2L),, was defined by
specifying some fraction, 6, of the undisturbed stress value below which the fiber
shall be considered ineffective. (X), normalized with fiber diameter, 2a, is derived as

where q5 is the portion of the fiber in which the average FAS is greater than 90% of
the stress that would exist for an infinite fiber. A plot of normalized ineffective
lengths is shown in Fig. 4.5 as a function of Young’s modulus ratio of the fiber to the

0,l y
100
10
3
Modulus ratio, 4 /E,.,,
Fig. 4.5. Normalized ineffective fiber length, (2L),/2a, as a function of modulus ratio, EfIE,,,, for varying
fiber volume fraction, 6. After Rosen (1964).