Page 271 - Engineered Interfaces in Fiber Reinforced Composites

252 Engineered interfaces in fiber reinforced composires

factor, of the composite. A is a ‘matrix stress condition factor’ which reflects changes
in the fracture toughness of matrix material due to the presence of the fibers and
specimen thickness; and B is related to the energy absorbing mechanisms of the
fibers and can be determined from the empirical linear relationship between K, and
Q. If R = 0, A becomes very close to 1, and thus K, % Km. However, if the measured
value of K, is higher than the real value due to specimen thickness, then 0 < A < 1.
If the fibers have a ductility-enhancing effect on the surrounding matrix, A becomes
greater than unity. B can be either positive or negative depending on the relative
magnitude between the loss of effective matrix toughness due to the presence of
fibers, i.e., (1 - vf)Km, and the increase in toughness due to other mechanisms, fiber
pull-out in particular. For very ductile matrices, e.g., PC and PTFE, B < 0; and for
moderately ductile thermoplastic matrices, e.g., PEEK, polyphenylene sulfide (PPS)
and low ductility polyethylene terephthalate (PET), B > 0 since toughness increase
due to the fiber pull-out mechanism is greater than the loss of matrix toughness as in
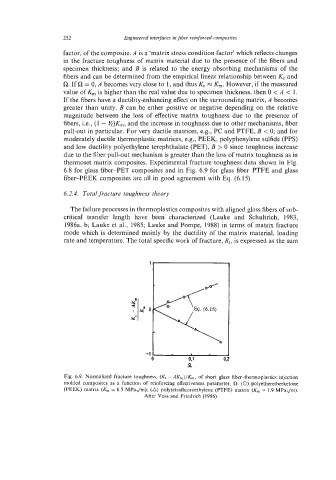
thermoset matrix composites. Experimental fracture toughness data shown in Fig.
6.8 for glass fiber-PET composites and in Fig. 6.9 for glass fiber-PTFE and glass
fiber-PEEK composites are all in good agreement with Eq. (6.15).

6.2.4. Total fracture toughness theory

The failure processes in thermoplastics composites with aligned glass fibers of sub-
critical transfer length have been characterized (Lauke and Schultrich, 1983,
1986a, b; Lauke et al., 1985; Lauke and Pompe, 1988) in terms of matrix fracture
mode which is determined mainly by the ductility of the matrix material, loading
rate and temperature. The total specific work of fracture, Rt, is expressed as the sum

%E
d
w
H
+EO< - 0 o c b. (6.15)
%-
\

-1 i