Page 183 - Entrophy Analysis in Thermal Engineering Systems

178 Entropy Analysis in Thermal Engineering Systems

Ψ fl T 0 S S 0 Þ
ð
η ¼ ¼ 1 (11.33)
max
H H 0 H H 0
To establish an expression for the maximum efficiency of an engine driven
by fuel combustion, we note that the thermal energy input per unit mole of
fuel is HHV n v L (see Eq. 8.11) and the maximum work is the chemical
w
0
exergy of the fuel given by Eq. (11.22). Hence,
C + F ΛðÞ
η ¼ (11.34)
max w
HHV n v L
0
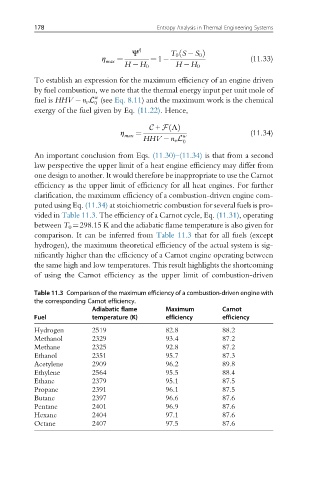
An important conclusion from Eqs. (11.30)–(11.34) is that from a second
law perspective the upper limit of a heat engine efficiency may differ from
one design to another. It would therefore be inappropriate to use the Carnot
efficiency as the upper limit of efficiency for all heat engines. For further
clarification, the maximum efficiency of a combustion-driven engine com-
puted using Eq. (11.34) at stoichiometric combustion for several fuels is pro-
vided in Table 11.3. The efficiency of a Carnot cycle, Eq. (11.31), operating
between T 0 ¼298.15 K and the adiabatic flame temperature is also given for
comparison. It can be inferred from Table 11.3 that for all fuels (except
hydrogen), the maximum theoretical efficiency of the actual system is sig-
nificantly higher than the efficiency of a Carnot engine operating between
the same high and low temperatures. This result highlights the shortcoming
of using the Carnot efficiency as the upper limit of combustion-driven

Table 11.3 Comparison of the maximum efficiency of a combustion-driven engine with
the corresponding Carnot efficiency.
Adiabatic flame Maximum Carnot
Fuel temperature (K) efficiency efficiency
Hydrogen 2519 82.8 88.2
Methanol 2329 93.4 87.2
Methane 2325 92.8 87.2
Ethanol 2351 95.7 87.3
Acetylene 2909 96.2 89.8
Ethylene 2564 95.5 88.4
Ethane 2379 95.1 87.5
Propane 2391 96.1 87.5
Butane 2397 96.6 87.6
Pentane 2401 96.9 87.6
Hexane 2404 97.1 87.6
Octane 2407 97.5 87.6