Page 46 - Entrophy Analysis in Thermal Engineering Systems

Teaching entropy 37

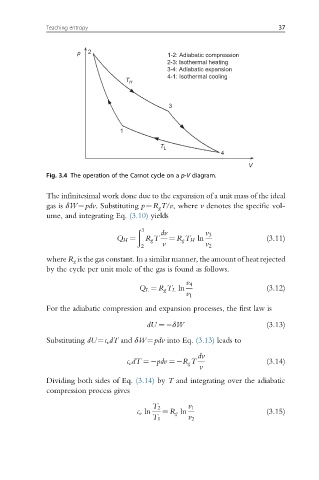
p 2 1-2: Adiabatic compression
2-3: Isothermal heating
3-4: Adiabatic expansion
T H 4-1: Isothermal cooling

3

1
T L
4
V
Fig. 3.4 The operation of the Carnot cycle on a p-V diagram.

The infinitesimal work done due to the expansion of a unit mass of the ideal
gas is δW¼pdv. Substituting p¼R g T/v, where v denotes the specific vol-
ume, and integrating Eq. (3.10) yields

ð 3
v 3
dv
Q H ¼ R g T ¼ R g T H ln (3.11)
2 v v 2
where R g is the gas constant. In a similar manner, the amount of heat rejected
by the cycle per unit mole of the gas is found as follows.

v 4
Q L ¼ R g T L ln (3.12)
v 1
For the adiabatic compression and expansion processes, the first law is
(3.13)
dU ¼ δW
Substituting dU¼c v dT and δW¼pdv into Eq. (3.13) leads to

dv
(3.14)
c v dT ¼ pdv ¼ R g T
v
Dividing both sides of Eq. (3.14) by T and integrating over the adiabatic
compression process gives

T 2 v 1
c v ln ¼ R g ln (3.15)
T 1 v 2