Page 48 - Entrophy Analysis in Thermal Engineering Systems

Teaching entropy 39

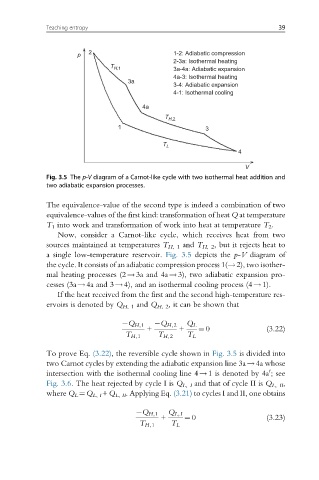
p 2 1-2: Adiabatic compression
2-3a: Isothermal heating
T H,1 3a-4a: Adiabatic expansion
4a-3: Isothermal heating
3a
3-4: Adiabatic expansion
4-1: Isothermal cooling
4a
T H,2
1 3

T L
4

V
Fig. 3.5 The p-V diagram of a Carnot-like cycle with two isothermal heat addition and
two adiabatic expansion processes.

The equivalence-value of the second type is indeed a combination of two
equivalence-values of the first kind: transformation of heat Q at temperature
T 1 into work and transformation of work into heat at temperature T 2 .
Now, consider a Carnot-like cycle, which receives heat from two
sources maintained at temperatures T H,1 and T H,2 , but it rejects heat to
a single low-temperature reservoir. Fig. 3.5 depicts the p-V diagram of
the cycle. It consists of an adiabatic compression process 1(!2), two isother-
mal heating processes (2!3a and 4a!3), two adiabatic expansion pro-
cesses (3a!4a and 3!4), and an isothermal cooling process (4!1).
If the heat received from the first and the second high-temperature res-
ervoirs is denoted by Q H,1 and Q H,2 , it can be shown that

Q H,1 Q H,2 Q L
+ + ¼ 0 (3.22)
T H,1 T H,2 T L

To prove Eq. (3.22), the reversible cycle shown in Fig. 3.5 is divided into
two Carnot cycles by extending the adiabatic expansion line 3a!4a whose
intersection with the isothermal cooling line 4!1 is denoted by 4a ; see
0
Fig. 3.6. The heat rejected by cycle I is Q L, I and that of cycle II is Q L, II ,
where Q L ¼Q L, I +Q L, II . Applying Eq. (3.21) to cycles I and II, one obtains

Q H,1 Q L,I
+ ¼ 0 (3.23)
T H,1 T L