Page 73 - Entrophy Analysis in Thermal Engineering Systems

Most efficient engine 65

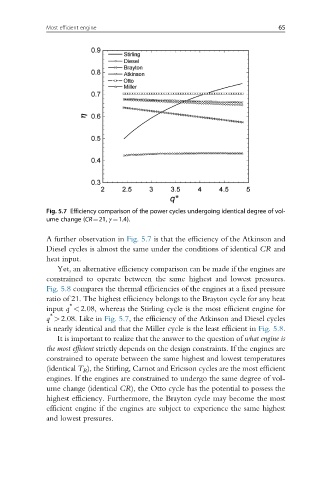
Fig. 5.7 Efficiency comparison of the power cycles undergoing identical degree of vol-
ume change (CR¼21, γ ¼1.4).

A further observation in Fig. 5.7 is that the efficiency of the Atkinson and
Diesel cycles is almost the same under the conditions of identical CR and
heat input.
Yet, an alternative efficiency comparison can be made if the engines are
constrained to operate between the same highest and lowest pressures.
Fig. 5.8 compares the thermal efficiencies of the engines at a fixed pressure
ratio of 21. The highest efficiency belongs to the Brayton cycle for any heat
∗
input q <2.08, whereas the Stirling cycle is the most efficient engine for
∗
q >2.08. Like in Fig. 5.7, the efficiency of the Atkinson and Diesel cycles
is nearly identical and that the Miller cycle is the least efficient in Fig. 5.8.

It is important to realize that the answer to the question of what engine is
the most efficient strictly depends on the design constraints. If the engines are
constrained to operate between the same highest and lowest temperatures
(identical T R ), the Stirling, Carnot and Ericsson cycles are the most efficient
engines. If the engines are constrained to undergo the same degree of vol-
ume change (identical CR), the Otto cycle has the potential to possess the
highest efficiency. Furthermore, the Brayton cycle may become the most
efficient engine if the engines are subject to experience the same highest
and lowest pressures.