Page 284 - Environmental Nanotechnology Applications and Impacts of Nanomaterials

Nanoparticle Transport, Aggregation, and Deposition 269

1
ap = 500 nm

0.1 ap = 100 nm
ap = 25 nm
0.01
Ai (µm 2 )

0.001

0.0001

0.00001
0.1 1 10 100
h (nm)
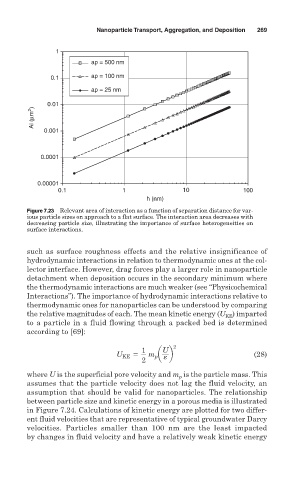
Figure 7.23 Relevant area of interaction as a function of separation distance for var-
ious particle sizes on approach to a flat surface. The interaction area decreases with
decreasing particle size, illustrating the importance of surface heterogeneities on
surface interactions.

such as surface roughness effects and the relative insignificance of
hydrodynamic interactions in relation to thermodynamic ones at the col-
lector interface. However, drag forces play a larger role in nanoparticle
detachment when deposition occurs in the secondary minimum where
the thermodynamic interactions are much weaker (see “Physicochemical
Interactions”). The importance of hydrodynamic interactions relative to
thermodynamic ones for nanoparticles can be understood by comparing
) imparted
the relative magnitudes of each. The mean kinetic energy (U KE
to a particle in a fluid flowing through a packed bed is determined
according to [69]:
2
1 U
U KE 5 m p a b (28)
e
2
where U is the superficial pore velocity and m is the particle mass. This
p
assumes that the particle velocity does not lag the fluid velocity, an
assumption that should be valid for nanoparticles. The relationship
between particle size and kinetic energy in a porous media is illustrated
in Figure 7.24. Calculations of kinetic energy are plotted for two differ-
ent fluid velocities that are representative of typical groundwater Darcy
velocities. Particles smaller than 100 nm are the least impacted
by changes in fluid velocity and have a relatively weak kinetic energy