Page 281 - Environmental Nanotechnology Applications and Impacts of Nanomaterials

266 Principles and Methods

–1
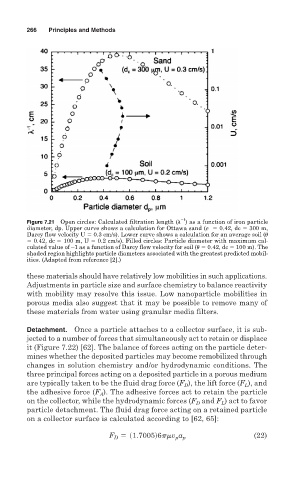
Figure 7.21 Open circles: Calculated filtration length ( ) as a function of iron particle
diameter, dp. Upper curve shows a calculation for Ottawa sand ( 0.42, dc 300 m,
Darcy flow velocity U 0.3 cm/s). Lower curve shows a calculation for an average soil (
0.42, dc 100 m, U 0.2 cm/s). Filled circles: Particle diameter with maximum cal-
culated value of –1 as a function of Darcy flow velocity for soil ( 0.42, dc 100 m). The
shaded region highlights particle diameters associated with the greatest predicted mobil-
ities. (Adapted from reference [2].)
these materials should have relatively low mobilities in such applications.
Adjustments in particle size and surface chemistry to balance reactivity
with mobility may resolve this issue. Low nanoparticle mobilities in
porous media also suggest that it may be possible to remove many of
these materials from water using granular media filters.

Detachment. Once a particle attaches to a collector surface, it is sub-
jected to a number of forces that simultaneously act to retain or displace
it (Figure 7.22) [62]. The balance of forces acting on the particle deter-
mines whether the deposited particles may become remobilized through
changes in solution chemistry and/or hydrodynamic conditions. The
three principal forces acting on a deposited particle in a porous medium
are typically taken to be the fluid drag force (F ), the lift force (F ), and
D
L
the adhesive force (F ). The adhesive forces act to retain the particle
A
on the collector, while the hydrodynamic forces (F and F ) act to favor
D
L
particle detachment. The fluid drag force acting on a retained particle
on a collector surface is calculated according to [62, 65]:
F 5 s1.7005d6pmv a (22)
D
p p