Page 302 - Fiber Fracture
P. 302
284 J.W.S. Hearle
Force
Po
h
D, Amplitude, y
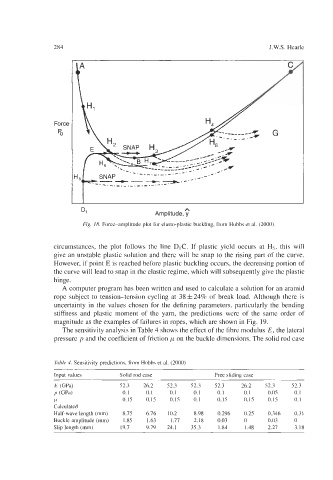
Fig. 18. Force-amplitude plot for elasto-plastic buckling, from Hobbs et al. (2000).
circumstances, the plot follows the line DIC. If plastic yield occurs at Hg, this will
give an unstable plastic solution and there will be snap to the rising part of the curve.
However, if point E is reached before plastic buckling occurs, the decreasing portion of
the curve will lead to snap in the elastic regime, which will subsequently give the plastic
hinge.
A computer program has been written and used to calculate a solution for an aramid
rope subject to tension-tension cycling at 38f24% of break load. Although there is
uncertainty in the values chosen for the defining parameters, particularly the bending
stiffness and plastic moment of the yarn, the predictions were of the same order of
magnitude as the examples of failures in ropes, which are shown in Fig. 19.
The sensitivity analysis in Table 4 shows the effect of the fibre modulus E, the lateral
pressure p and the coefficient of friction p on the buckle dimensions. The solid rod case
Table 4. Sensitivity predictions, from Hobbs et al. (2000)
Input values Solid rod case Free sliding case
E (GPa) 52.3 26.2 52.3 52.3 52.3 26.2 52.3 52.3
P (GPa) 0.1 0.1 0.1 0.1 0.1 0.1 0.05 0.1
w 0.15 0.15 0.15 0.1 0.15 0.15 0.15 0.1
Calculated
Half-wave length (mm) 8.75 6.76 10.2 8.98 0.296 0.25 0.346 0.31
Buckle amplitude (mm) 1.85 1.63 1.77 2.18 0.03 0 0.03 0
Slip length (mm) 19.7 9.79 24.1 35.3 1.84 1.48 2.21 3.18