Page 298 - Fiber Fracture

280 J.W.S. Hearle

100
8
5
ul
E 75
c
v)
a,
>
.-
c
% 50
U
0 100 200 300
Temperature “C

0 0.5 1
Fraction of 1 second break load
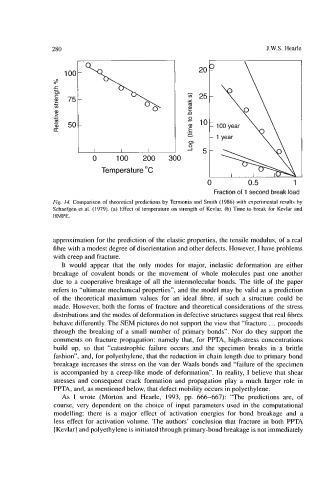
Fig. 14. Comparison of theoretical predictions by Termonia and Smith (1986) with experimental results by
Schaefgen et al. (1979). (a) Effect of temperature on strength of Kevlar. (b) Time to break for Kevlar and
HMPE.

approximation for the prediction of the elastic properties, the tensile modulus, of a real
fibre with a modest degree of disorientation and other defects. However, I have problems
with creep and fracture.
It would appear that the only modes for major, inelastic deformation are either
breakage of covalent bonds or the movement of whole molecules past one another
due to a cooperative breakage of all the intermolecular bonds. The title of the paper
refers to “ultimate mechanical properties”, and the model may be valid as a prediction
of the theoretical maximum values for an ideal fibre, if such a structure could be
made. However, both the forms of fracture and theoretical considerations of the stress
distributions and the modes of deformation in defective structures suggest that real fibres
behave differently. The SEM pictures do not support the view that “fracture . . . proceeds
through the breaking of a small number of primary bonds”. Nor do they support the
comments on fracture propagation: namely that, for PPTA, high-stress concentrations
build up, so that “catastrophic failure occurs and the specimen breaks in a brittle
fashion”, and, for polyethylene, that the reduction in chain length due to primary bond
breakage increases the stress on the van der Waals bonds and “failure of the specimen
is accompanied by a creep-like mode of deformation”. In reality, I believe that shear
stresses and consequent crack formation and propagation play a much larger role in
PPTA, and, as mentioned below, that defect mobility occurs in polyethylene.
As I wrote (Morton and Hearle, 1993, pp. 666-667): “The predictions are, of
course, very dependent on the choice of input parameters used in the computational
modelling: there is a major effect of activation energies for bond breakage and a
less effect for activation volume. The authors’ conclusion that fracture in both PPTA
[Kevlar] and polyethylene is initiated through primary-bond breakage is not immediately