Page 319 - Fiber Fracture

FRACTURE OF SYNTHETIC POLYMER FIBERS 301
10
.‘\h
0. Slope = -0.42

-0

1-
0
00

1 I
0

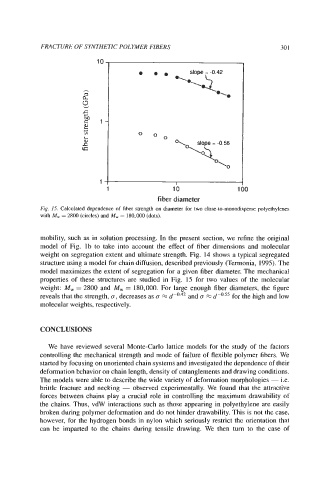
Fig. 15. Calculated dependence of fiber strength on diameter for two close-to-monodisperse polyethylenes
with M, = 2800 (circles) and M, = 180,ooO (dots).

mobility, such as in solution processing. In the present section, we refine the original
model of Fig. lb to take into account the effect of fiber dimensions and molecular
weight on segregation extent and ultimate strength. Fig. 14 shows a typical segregated
structure using a model for chain diffusion, described previously (Termonia, 1995). The
model maximizes the extent of segregation for a given fiber diameter. The mechanical
properties of these structures are studied in Fig. 15 for two values of the molecular
weight: M, = 2800 and M, = 180,000. For large enough fiber diameters, the figure
reveals that the strength, u, decreases as u d-0.42 and u x d-0.55 for the high and low
molecular weights, respectively.

CONCLUSIONS

We have reviewed several Monte-Carlo lattice models for the study of the factors
controlling the mechanical strength and mode of failure of flexible polymer fibers. We
started by focusing on unoriented chain systems and investigated the dependence of their
deformation behavior on chain length, density of entanglements and drawing conditions.
The models were able to describe the wide variety of deformation morphologies - Le.
brittle fracture and necking - observed experimentally. We found that the attractive
forces between chains play a crucial role in controlling the maximum drawability of
the chains. Thus, vdW interactions such as those appearing in polyethylene are easily
broken during polymer deformation and do not hinder drawability. This is not the case,
however, for the hydrogen bonds in nylon which seriously restrict the orientation that
can be imparted to the chains during tensile drawing. We then turn to the case of