Page 361 - Fiber Fracture

343

0 10 20 30 40
Extension %
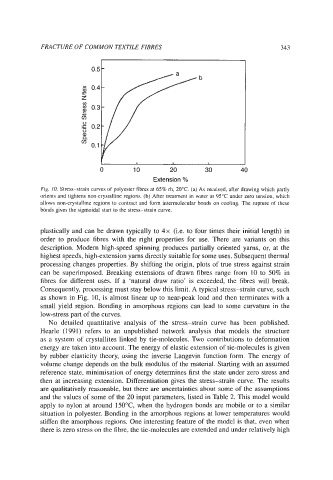
Fig. IO. Stress-strain curves of polyester fibres at 65% rh, 20°C. (a) As received, after drawing which partly
orients and tightens non-crystalline regions. (b) After treatment in water at 95°C under zero tension, which
allows non-crystalline regions to contract and form intermolecular bonds on cooling. The rupture of these
bonds gives the sigmoidal start to the stress-strain curve.

plastically and can be drawn typically to 4x (Le. to four times their initial length) in
order to produce fibres with the right properties for use. There are variants on this
description. Modem high-speed spinning produces partially oriented yams, or, at the
highest speeds, high-extension yams directly suitable for some uses. Subsequent thermal
processing changes properties. By shifting the origin, plots of true stress against strain
can be superimposed. Breaking extensions of drawn fibres range from 10 to 50% in
fibres for different uses. If a 'natural draw ratio' is exceeded, the fibres will break.
Consequently, processing must stay below this limit. A typical stress-strain curve, such
as shown in Fig. 10, is almost linear up to near-peak load and then terminates with a
small yield region. Bonding in amorphous regions can lead to some curvature in the
low-stress part of the curves.
No detailed quantitative analysis of the stress-strain curve has been published.
Hearle (1991) refers to an unpublished network analysis that models the structure
as a system of crystallites linked by tie-molecules. Two contributions to deformation
energy are taken into account. The energy of elastic extension of tie-molecules is given
by rubber elasticity theory, using the inverse Langevin function form. The energy of
volume change depends on the bulk modulus of the material. Starting with an assumed
reference state, minimisation of energy determines first the state under zero stress and
then at increasing extension. Differentiation gives the stress-strain curve. The results
are qualitatively reasonable, but there are uncertainties about some of the assumptions
and the values of some of the 20 input parameters, listed in Table 2. This model would
apply to nylon at around 150°C, when the hydrogen bonds are mobile or to a similar
situation in polyester. Bonding in the amorphous regions at lower temperatures would
stiffen the amorphous regions. One interesting feature of the model is that, even when
there is zero stress on the fibre, the tie-molecules are extended and under relatively high