Page 67 - Fiber Fracture

52 M. Elices and J. Llorca

2x = 0.01 L
0 -
0 I \
X
cu
v t '?
a
0
4- \
I *\

CT =CT
b O
2x = L

0
3 5 10 30 50 100
Wibull modulus, m
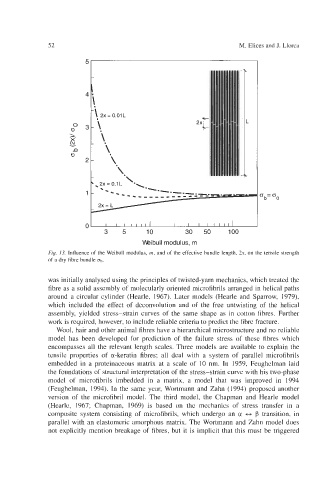
Fig. 13. Influence of the Weibull modulus, m, and of the effective bundle length, 2x, on the tensile strength
of a dry fibre bundle ab.

was initially analysed using the principles of twisted-yam mechanics, which treated the
fibre as a solid assembly of molecularly oriented microfibrils arranged in helical paths
around a circular cylinder (Hearle, 1967). Later models (Hearle and Sparrow, 1979),
which included the effect of deconvolution and of the free untwisting of the helical
assembly, yielded stress-strain curves of the same shape as in cotton fibres. Further
work is required, however, to include reliable criteria to predict the fibre fracture.
Wool, hair and other animal fibres have a hierarchical microstructure and no reliable
model has been developed for prediction of the failure stress of these fibres which
encompasses all the relevant length scales. Three models are available to explain the
tensile properties of a-keratin fibres; all deal with a system of parallel microfibrils
embedded in a proteinaceous matrix at a scale of 10 nm. In 1959, Feughelman laid
the foundations of structural interpretation of the stress-strain curve with his two-phase
model of microfibrils imbedded in a matrix, a model that was improved in 1994
(Feughelman, 1994). In the same year, Wortmann and Zahn (1994) proposed another
version of the microfibril model. The third model, the Chapman and Hearle model
(Hearle, 1967; Chapman, 1969) is based on the mechanics of stress transfer in a
composite system consisting of microfibrils, which undergo an a t, B transition, in
parallel with an elastomeric amorphous matrix. The Wortmann and Zahn model does
not explicitly mention breakage of fibres, but it is implicit that this must be triggered