Page 65 - Fiber Fracture

50 M. Elices and J. Llorca

\k
r c
1 .o I I I I I
0.0 0.5 1 .o 1.5 2.0 2.5 3.0
d/r
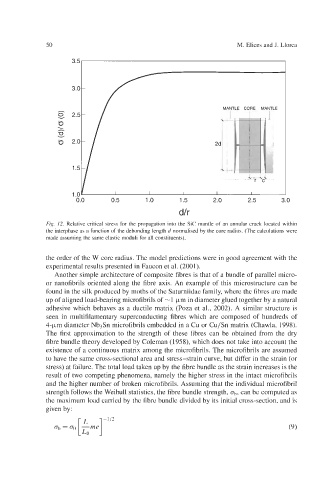
Fig. 12. Relative critical stress for the propagation into the Sic mantle of an annular crack located within
the interphase as a function of the debonding length d normalised by the core radius. (The calculations were
made assuming the same elastic moduli for all constituents).

the order of the W core radius. The model predictions were in good agreement with the
experimental results presented in Faucon et al. (2001).
Another simple architecture of composite fibres is that of a bundle of parallel micro-
or nanofibrils oriented along the fibre axis. An example of this microstructure can be
found in the silk produced by moths of the Saturniidae family, where the fibres are made
up of aligned load-bearing microfibrils of -1 wm in diameter glued together by a natural
adhesive which behaves as a ductile matrix (Poza et al., 2002). A similar structure is
seen in multifilamentary superconducting fibres which are composed of hundreds of
4-km diameter Nb3Sn microfibrils embedded in a Cu or Cu/Sn matrix (Chawla, 1998).
The first approximation to the strength of these fibres can be obtained from the dry
fibre bundle theory developed by Coleman (1958), which does not take into account the
existence of a continuous matrix among the microfibrils. The microfibrils are assumed
to have the same cross-sectional area and stress-strain curve, but differ in the strain (or
stress) at failure. The total load taken up by the fibre bundle as the strain increases is the
result of two competing phenomena, namely the higher stress in the intact microfibrils
and the higher number of broken microfibrils. Assuming that the individual microfibril
strength follows the Weibull statistics, the fibre bundle strength, ab, can be computed as
the maximum load carried by the fibre bundle divided by its initial cross-section, and is
given by: