Page 505 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

EXPERIMENTAL METHODS FOR ELASTOMER PIPES 475

Q,, and the logarithmic decrement, 61, are measured. These are then compared with
the theoretical values, to determine EZ and the damping constants; this is done in an
indirect manner, as described in what follows, since i21 and 61 are functions of the
gravity parameter, y. In the experiments the decaying pipe vibration can be sensed by a
fibre-optic sensor or an optical tracking system (Section 5.8. l), both noncontacting, the
signal from which can be processed electronically; see also Section D.4.
The equation of motion of the vertical empty pipe is a simplified form of (3.70), namely

the complex eigenfrequencies of which, wi = %e(wi) + i.Yjam(oi), and hence the
logarithmic decrement Ai = 2n9m(wi)/%e(wi), may be found for any y by the method
of Section 3.3.6(b). In this way, Figure D.3 is constructed, for the first mode, i = 1.
The dashed line in this figure is from a Rayleigh method approximation, yielding
[%e(w)I2/y = (81/52) + (162/13y).
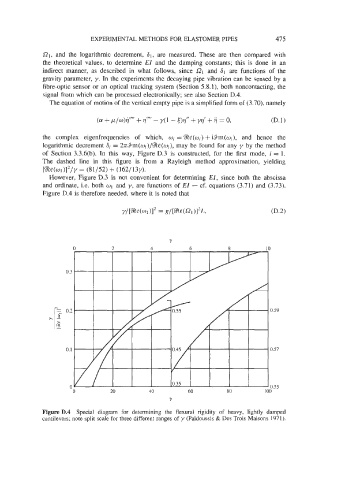
However, Figure D.3 is not convenient for determining EZ, since both the abscissa
and ordinate, i.e. both w1 and y, are functions of EZ - cf. equations (3.71) and (3.73).
Figure D.4 is therefore needed, where it is noted that

Y
Figure D.4 Special diagram for determining the flexural rigidity of heavy, lightly damped
cantilevers; note split scale for three different ranges of y (Paidoussis & Des Trois Maisons 1971).