Page 309 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C006.fm Page 289 Monday, May 23, 2005 5:50 PM

Fracture Mechanisms in Nonmetals 289

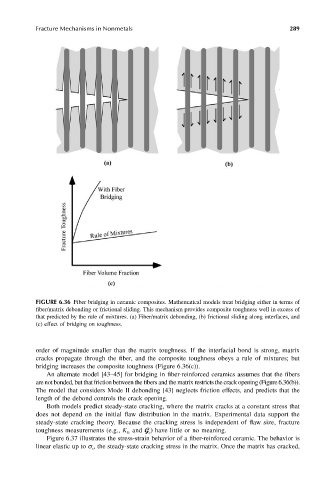
FIGURE 6.36 Fiber bridging in ceramic composites. Mathematical models treat bridging either in terms of
fiber/matrix debonding or frictional sliding. This mechanism provides composite toughness well in excess of
that predicted by the rule of mixtures. (a) Fiber/matrix debonding, (b) frictional sliding along interfaces, and
(c) effect of bridging on toughness.

order of magnitude smaller than the matrix toughness. If the interfacial bond is strong, matrix
cracks propagate through the fiber, and the composite toughness obeys a rule of mixtures; but
bridging increases the composite toughness (Figure 6.36(c)).
An alternate model [43–45] for bridging in fiber-reinforced ceramics assumes that the fibers
are not bonded, but that friction between the fibers and the matrix restricts the crack opening (Figure 6.36(b)).
The model that considers Mode II debonding [43] neglects friction effects, and predicts that the
length of the debond controls the crack opening.
Both models predict steady-state cracking, where the matrix cracks at a constant stress that
does not depend on the initial flaw distribution in the matrix. Experimental data support the
steady-state cracking theory. Because the cracking stress is independent of flaw size, fracture
toughness measurements (e.g., K and G ) have little or no meaning.
Ic
c
Figure 6.37 illustrates the stress-strain behavior of a fiber-reinforced ceramic. The behavior is
linear elastic up to σ , the steady-state cracking stress in the matrix. Once the matrix has cracked,
c