Page 409 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C009.fm Page 389 Monday, May 23, 2005 3:58 PM

Application to Structures 389

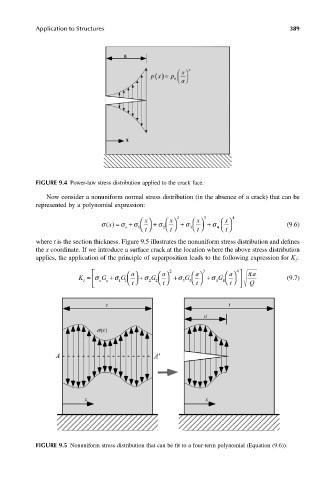
FIGURE 9.4 Power-law stress distribution applied to the crack face.

Now consider a nonuniform normal stress distribution (in the absence of a crack) that can be
represented by a polynomial expression:

σ σ() x = o + σ 1  x  + σ 2  x  2 + σ 3  x  3 + σ 4  x  4 (9.6)
t  
t  
t  
t  
where t is the section thickness. Figure 9.5 illustrates the nonuniform stress distribution and defines
the x coordinate. If we introduce a surface crack at the location where the above stress distribution
applies, the application of the principle of superposition leads to the following expression for K :
I
  a   a  2  a  3  a  4  π a
K I o G = o  + σ σ G +σ G +σ G +σ G  (9.7)
 11 t   2 2 t   3 3 t   4 4 t    Q

FIGURE 9.5 Nonuniform stress distribution that can be fit to a four-term polynomial (Equation (9.6)).