Page 83 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C02.fm Page 63 Thursday, April 14, 2005 6:28 PM

Linear Elastic Fracture Mechanics 63

Elliptical and semielliptical flaws (Figure 2.20) also have an approximate closed-form plastic zone
correction, provided the flaw is small compared to the plate dimensions. In the case of the embedded
elliptical flaw, K is given by
eff

π a   a  2  / 14
K eff = Q eff   sin 2 φ + σ  c  cos ( )   (2.71)
2
φ ( )
where Q is the effective flaw shape parameter defined as
eff

 σ  2
Q eff Q = − 0 212   σ YS   (2.72)
.

Equation (2.72) must be multiplied by a surface correction factor for a semielliptical surface
flaw (see Figure 2.20).
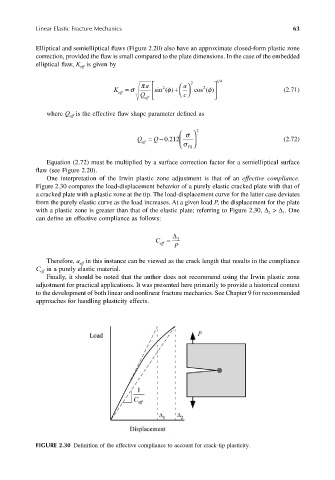
One interpretation of the Irwin plastic zone adjustment is that of an effective compliance.
Figure 2.30 compares the load-displacement behavior of a purely elastic cracked plate with that of
a cracked plate with a plastic zone at the tip. The load-displacement curve for the latter case deviates
from the purely elastic curve as the load increases. At a given load P, the displacement for the plate
with a plastic zone is greater than that of the elastic plate; referring to Figure 2.30, ∆ > ∆ . One
1
2
can define an effective compliance as follows:
∆
C = P 2
eff

Therefore, a in this instance can be viewed as the crack length that results in the compliance
eff
C in a purely elastic material.
eff
Finally, it should be noted that the author does not recommend using the Irwin plastic zone
adjustment for practical applications. It was presented here primarily to provide a historical context
to the development of both linear and nonlinear fracture mechanics. See Chapter 9 for recommended
approaches for handling plasticity effects.

FIGURE 2.30 Definition of the effective compliance to account for crack-tip plasticity.