Page 86 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C02.fm Page 66 Thursday, April 14, 2005 6:28 PM

66 Fracture Mechanics: Fundamentals and Applications

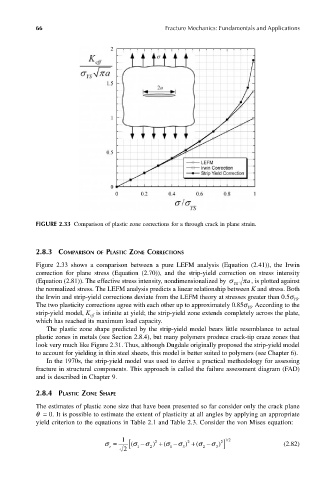
FIGURE 2.33 Comparison of plastic zone corrections for a through crack in plane strain.

2.8.3 COMPARISON OF PLASTIC ZONE CORRECTIONS

Figure 2.33 shows a comparison between a pure LEFM analysis (Equation (2.41)), the Irwin
correction for plane stress (Equation (2.70)), and the strip-yield correction on stress intensity
(Equation (2.81)). The effective stress intensity, nondimensionalized by σ YS π a , is plotted against
the normalized stress. The LEFM analysis predicts a linear relationship between K and stress. Both
the Irwin and strip-yield corrections deviate from the LEFM theory at stresses greater than 0.5σ .
YS
The two plasticity corrections agree with each other up to approximately 0.85σ . According to the
YS
strip-yield model, K is infinite at yield; the strip-yield zone extends completely across the plate,
eff
which has reached its maximum load capacity.
The plastic zone shape predicted by the strip-yield model bears little resemblance to actual
plastic zones in metals (see Section 2.8.4), but many polymers produce crack-tip craze zones that
look very much like Figure 2.31. Thus, although Dugdale originally proposed the strip-yield model
to account for yielding in thin steel sheets, this model is better suited to polymers (see Chapter 6).
In the 1970s, the strip-yield model was used to derive a practical methodology for assessing
fracture in structural components. This approach is called the failure assessment diagram (FAD)
and is described in Chapter 9.

2.8.4 PLASTIC ZONE SHAPE
The estimates of plastic zone size that have been presented so far consider only the crack plane
θ = 0. It is possible to estimate the extent of plasticity at all angles by applying an appropriate
yield criterion to the equations in Table 2.1 and Table 2.3. Consider the von Mises equation:

σ 1 σ = σ [ 2 σ− σ + ( 2 ( σ− ) − ) σ + ( ) 2 ] 12 / (2.82)
e
2 1 2 1 3 2 3