Page 173 - Fundamentals of Communications Systems

Analog Communications Basics 5.13

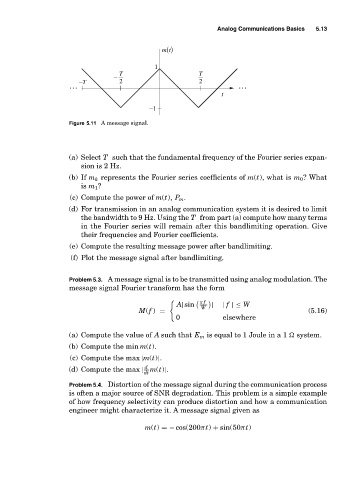
mt ()

1
− T T
… −T 2 2 …
t

−1
Figure 5.11 A message signal.

(a) Select T such that the fundamental frequency of the Fourier series expan-
sion is 2 Hz.
(b) If m k represents the Fourier series coefficients of m(t), what is m 0 ? What
is m 1 ?
(c) Compute the power of m(t), P m .
(d) For transmission in an analog communication system it is desired to limit
the bandwidth to 9 Hz. Using the T from part (a) compute how many terms
in the Fourier series will remain after this bandlimiting operation. Give
their frequencies and Fourier coefficients.
(e) Compute the resulting message power after bandlimiting.
(f) Plot the message signal after bandlimiting.

Problem 5.3. A message signal is to be transmitted using analog modulation. The
message signal Fourier transform has the form
π f
A| sin | | f |≤ W
W
M(f ) = (5.16)
0 elsewhere
(a) Compute the value of A such that E m is equal to 1 Joule in a 1 system.
(b) Compute the min m(t).
(c) Compute the max |m(t)|.
d
(d) Compute the max | m(t)|.
dt
Problem 5.4. Distortion of the message signal during the communication process
is often a major source of SNR degradation. This problem is a simple example
of how frequency selectivity can produce distortion and how a communication
engineer might characterize it. A message signal given as

m(t) =− cos(200πt) + sin(50πt)