Page 178 - Fundamentals of Computational Geoscience Numerical Methods and Algorithms

168 7 Simulating Thermal and Chemical Effects of Intruded Magma Solidification Problems

hybrid 1D-2D model may avoid the need to introduce equivalent volumetric heat and
mass source terms. However, since the 1D and 2D models are considered separately
and interactively, one must use the 1D model to determine the temperature and ther-
mal flux boundary conditions on the solidification interface between the rock and
intruded magma, and then apply such boundary conditions to the 2D model for sim-
ulating the thermal field in the surrounding rocks. Since the magma solidification is
time-dependent, the above-mentioned boundary conditions need to be determined
and applied in the hybrid 1D-2D model repeatedly for each time step during the
intruded magma solidification. This certainly adds numerical modelling complexity
during the magma solidification, because the previous boundary conditions must be
modified and the current ones must be applied to the 2D model. This complexity
has been avoided by using the proposed numerical algorithm in this study, since
the magma solidification in the intruded magma region and heat transfer in the sur-
rounding rocks are considered simultaneously, rather than separately, in the finite
element analysis. Due to this obvious advantage in using the proposed model, there
is no need to develop the hybrid 1D-2D model for simulating the solidification prob-
lems associated with intruded magma dikes and sills.
After the verification of the proposed equivalent source algorithm for simulat-
ing solidification effects of dike-like magma intrusion problems in porous rocks,
it has been applied to investigate the chemical effects of a dike-like magma intru-
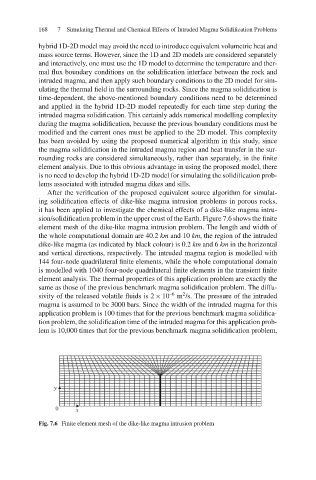
sion/solidification problem in the upper crust of the Earth. Figure 7.6 shows the finite
element mesh of the dike-like magma intrusion problem. The length and width of
the whole computational domain are 40.2 km and 10 km, the region of the intruded
dike-like magma (as indicated by black colour) is 0.2 km and 6 km in the horizontal
and vertical directions, respectively. The intruded magma region is modelled with
144 four-node quadrilateral finite elements, while the whole computational domain
is modelled with 1040 four-node quadrilateral finite elements in the transient finite
element analysis. The thermal properties of this application problem are exactly the
same as those of the previous benchmark magma solidification problem. The diffu-
2
sivity of the released volatile fluids is 2 × 10 –6 m /s. The pressure of the intruded
magma is assumed to be 3000 bars. Since the width of the intruded magma for this
application problem is 100 times that for the previous benchmark magma solidifica-
tion problem, the solidification time of the intruded magma for this application prob-
lem is 10,000 times that for the previous benchmark magma solidification problem,

y

0 x

Fig. 7.6 Finite element mesh of the dike-like magma intrusion problem