Page 87 - Fundamentals of Probability and Statistics for Engineers

70 Fundamentals of Probability and Statistics for Engineers

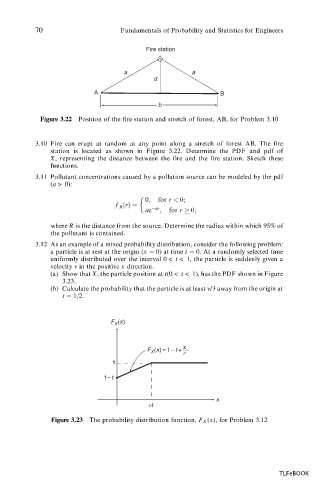
Fire station

a a
d
A B
b

Figure 3.22 Position of the fire station and stretch of forest, AB, for Problem 3.10

3.10 Fire can erupt at random at any point along a stretch of forest AB. The fire
station is located as shown in Figure 3.22. Determine the PDF and pdf of
X, representing the distance between the fire and the fire station. Sketch these
functions.
3.11 Pollutant concentrations caused by a pollution source can be modeled by the pdf
(a > 0):
0; for r < 0;

f r†ˆ
R ar
ae ; for r 0;
where R is the distance from the source. Determine the radius within which 95% of
the pollutant is contained.
3.12 As an example of a mixed probability distribution, consider the following problem:
a particle is at rest at the origin (x ˆ 0) at time t ˆ 0. At a randomly selected time
uniformly distributed over the interval 0 < t < 1, the particle is suddenly given a
velocity v in the positive x direction.
(a) Show that X, the particle position at t(0 < t < 1), has the PDF shown in Figure
3.23.
(b) Calculate the probability that the particle is at least v/3 away from the origin at
t ˆ 1/2.

F (x)
X

x
F (x)=1– t +—
ν
X
1
1– t

x
t ν

Figure 3.23 The probability distribution function, F X (x), for Problem 3.12

TLFeBOOK