Page 85 - Fundamentals of Probability and Statistics for Engineers

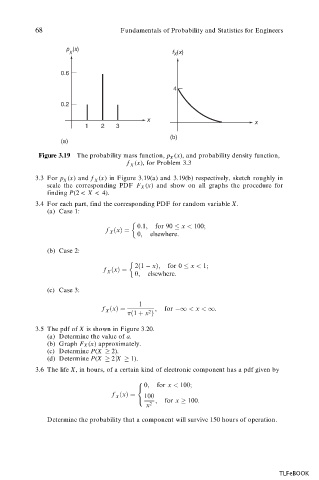
68 Fundamentals of Probability and Statistics for Engineers

p (x)
X f (x)
X
0.6

4
0.2

x x
1 2 3
(b)
(a)

Figure 3.19 The probability mass function, p (x), and probability density function,
X
f (x), for Problem 3.3
X
3.3 For p (x) and f (x) in Figure 3.19(a) and 3.19(b) respectively, sketch roughly in
X
X
scale the corresponding PDF F X (x) and show on all graphs the procedure for
finding P(2 < X < 4).
3.4 For each part, find the corresponding PDF for random variable X.
(a) Case 1:
0:1; for 90 x < 100;

f x†ˆ
X 0; elsewhere:
(b) Case 2:

2 1 x†; for 0 x < 1;
f x†ˆ 0; elsewhere:
X
(c) Case 3:
1
f x†ˆ ; for 1 < x < 1:
X
2
1 ‡ x †
3.5 The pdf of X is shown in Figure 3.20.
(a) Determine the value of a.
(b) Graph F X (x) approximately.
(c) Determine P(X 2).
2 X
(d) Determine P(X j 1).
3.6 The life X, in hours, of a certain kind of electronic component has a pdf given by
0; for x < 100;
8
<
f x†ˆ 100
X
: ; for x 100:
x 2
Determine the probability that a component will survive 150 hours of operation.

TLFeBOOK