Page 256 - Fundamentals of Radar Signal Processing
P. 256
Integrating the slow-time samples gives
(4.69)
Equation (4.69) gives the system response to the pulse burst waveform in an
arbitrary range bin l as a function of the normalized Doppler mismatch ω .
D
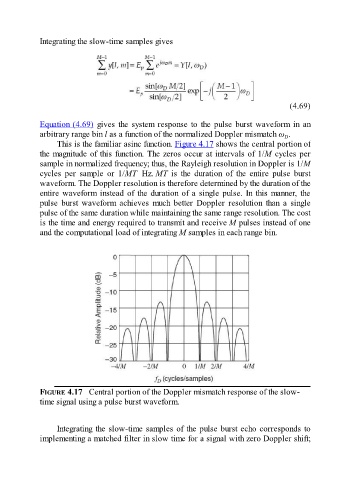
This is the familiar asinc function. Figure 4.17 shows the central portion of
the magnitude of this function. The zeros occur at intervals of 1/M cycles per
sample in normalized frequency; thus, the Rayleigh resolution in Doppler is 1/M
cycles per sample or 1/MT Hz. MT is the duration of the entire pulse burst
waveform. The Doppler resolution is therefore determined by the duration of the
entire waveform instead of the duration of a single pulse. In this manner, the
pulse burst waveform achieves much better Doppler resolution than a single
pulse of the same duration while maintaining the same range resolution. The cost
is the time and energy required to transmit and receive M pulses instead of one
and the computational load of integrating M samples in each range bin.
FIGURE 4.17 Central portion of the Doppler mismatch response of the slow-
time signal using a pulse burst waveform.
Integrating the slow-time samples of the pulse burst echo corresponds to
implementing a matched filter in slow time for a signal with zero Doppler shift;