Page 314 - Fundamentals of Radar Signal Processing

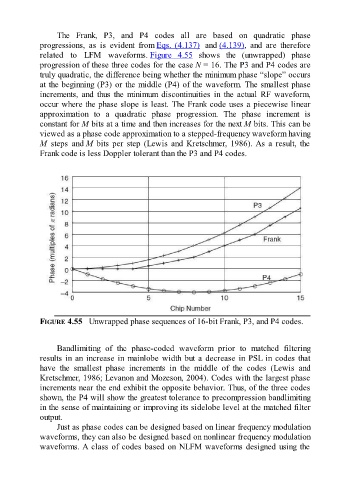
The Frank, P3, and P4 codes all are based on quadratic phase
progressions, as is evident from Eqs. (4.137) and (4.139), and are therefore
related to LFM waveforms. Figure 4.55 shows the (unwrapped) phase

progression of these three codes for the case N = 16. The P3 and P4 codes are
truly quadratic, the difference being whether the minimum phase “slope” occurs
at the beginning (P3) or the middle (P4) of the waveform. The smallest phase
increments, and thus the minimum discontinuities in the actual RF waveform,
occur where the phase slope is least. The Frank code uses a piecewise linear
approximation to a quadratic phase progression. The phase increment is
constant for M bits at a time and then increases for the next M bits. This can be

viewed as a phase code approximation to a stepped-frequency waveform having
M steps and M bits per step (Lewis and Kretschmer, 1986). As a result, the
Frank code is less Doppler tolerant than the P3 and P4 codes.

FIGURE 4.55 Unwrapped phase sequences of 16-bit Frank, P3, and P4 codes.

Bandlimiting of the phase-coded waveform prior to matched filtering
results in an increase in mainlobe width but a decrease in PSL in codes that
have the smallest phase increments in the middle of the codes (Lewis and
Kretschmer, 1986; Levanon and Mozeson, 2004). Codes with the largest phase
increments near the end exhibit the opposite behavior. Thus, of the three codes
shown, the P4 will show the greatest tolerance to precompression bandlimiting

in the sense of maintaining or improving its sidelobe level at the matched filter
output.
Just as phase codes can be designed based on linear frequency modulation
waveforms, they can also be designed based on nonlinear frequency modulation
waveforms. A class of codes based on NLFM waveforms designed using the