Page 315 - Fundamentals of Radar Signal Processing

PSP technique mentioned earlier is given in Felhauer (1994). No closed form

expression is known for these P(n, k) codes; they must be found numerically.
Typical results are very similar to those for the empirical NLFM waveforms
described earlier. The effect of Doppler mismatch is similar to that observed in
Fig. 4.39. This is an improvement over conventional polyphase codes, which
are prone to exhibiting significantly increased sidelobes near the ends of the
code and, in many cases, large spurious peaks well above the general sidelobe

level. P(n, k) codes also exhibit better tolerance to precompression
bandlimiting than do codes based on linear FM, since their spectra are already
shaped by the basic NLFM design approach. Their chief disadvantage is the
difficulty of their design.
Another approach to reducing spectral sidelobes and thus improving
precompression bandlimiting tolerance is the use of quadriphase codes. These
codes are obtained from biphase codes by mapping the binary phase

progression to a four-phase code using a specified transformation, and also by
replacing the rectangular subpulse chips with half-cosine chips of twice the
width. Compared to the biphase code, the resulting codes have significantly
lower spectral sidelobes, nearly the same autocorrelation sidelobes, but a
significant loss of time (range) resolution. Details are given in Keel and Baden
(2012).

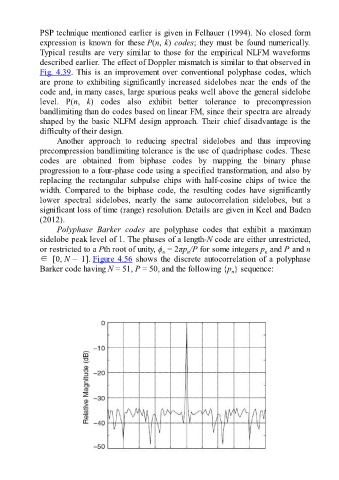
Polyphase Barker codes are polyphase codes that exhibit a maximum
sidelobe peak level of 1. The phases of a length-N code are either unrestricted,
or restricted to a Pth root of unity, ϕ = 2πp /P for some integers p and P and n
n
n
n
∈ [0, N – 1]. Figure 4.56 shows the discrete autocorrelation of a polyphase
Barker code having N = 51, P = 50, and the following {p } sequence:
n