Page 662 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

Disinfection 617

Example 19.2 Apply the Watson–Chick Relations 19.3.2.1 Examples of C ? t Relation
to Determine C ? t for 99% Kill, That Is, C ? t(99%
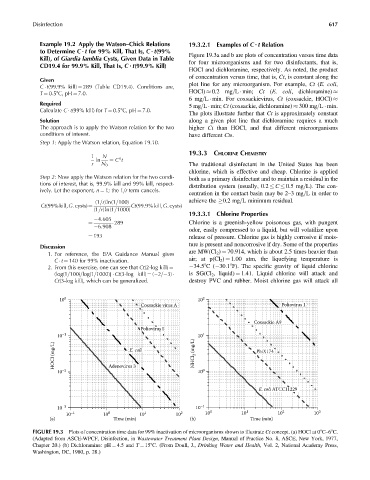
Kill), of Giardia lamblia Cysts, Given Data in Table Figure 19.3a and b are plots of concentration versus time data
CD19.4 for 99.9% Kill, That Is, C ? t(99.9% Kill) for four microorganisms and for two disinfectants, that is,
HOCl and dichloramine, respectively. As noted, the product
of concentration versus time, that is, Ct, is constant along the
Given
plot line for any microorganism. For example, Ct (E. coli,
C t(99.9% kill) ¼ 289 (Table CD19.4). Conditions are,
T ¼ 0.58C, pH ¼ 7.0. HOCl) 0.2 mg=L min; Ct (E. coli, dichloramine)
6mg=L min. For coxsackievirus, Ct (coxsackie, HOCl)
Required
5mg=L min; Ct (coxsackie, dichloramine) 300 mg=L min.
Calculate C t(99% kill) for T ¼ 0.58C, pH ¼ 7.0.
The plots illustrate further that Ct is approximately constant
Solution along a given plot line that dichloramine requires a much
The approach is to apply the Watson relation for the two higher Ct than HOCl, and that different microorganisms
conditions of interest. have different Cts.
Step 1: Apply the Watson relation, Equation 19.10.
19.3.3 CHLORINE CHEMISTRY
1 N n
ln ¼ C t
r N 0 The traditional disinfectant in the United States has been
chlorine, which is effective and cheap. Chlorine is applied
Step 2: Now apply the Watson relation for the two condi- both as a primary disinfectant and to maintain a residual in the
tions of interest, that is, 99.9% kill and 99% kill, respect- distribution system (usually, 0.2 C 0.5 mg=L). The con-
ively. Let the exponent, n ¼ 1; the 1=r term cancels.
centration in the contact basin may be 2–3mg=L in order to
(1=r)ln(1=100) achieve the 0.2 mg=L minimum residual.
Ct(99:9% kill,G:cysts)
(1=r)ln(1=1000)
Ct(99% kill,G:cysts)¼
19.3.3.1 Chlorine Properties
4:605
289 Chlorine is a greenish-yellow poisonous gas, with pungent
6:908
¼
odor, easily compressed to a liquid, but will volatilize upon
¼ 193 release of pressure. Chlorine gas is highly corrosive if mois-
ture is present and noncorrosive if dry. Some of the properties
Discussion
are MW(Cl 2 ) ¼ 70.914, which is about 2.5 times heavier than
1. For reference, the EPA Guidance Manual gives
C t ¼ 140 for 99% inactivation. air; at p(Cl 2 ) ¼ 1.00 atm, the liquefying temperature is
34.58C( 30.18F). The specific gravity of liquid chlorine
2. From this exercise, one can see that Ct(2-log kill) ¼
is SG(Cl 2 , liquid) ¼ 1.41. Liquid chlorine will attack and
(log(1=100)=log(1=1000)] Ct(3-log kill) ¼ ( 2= 3)
Ct(3-log kill), which can be generalized. destroy PVC and rubber. Moist chlorine gas will attack all
10 0 10 2
Coxsackie virus A Poliovirus 1

Coxsackie A9
Poliovirus I
10 –1 10 1
HOCl (mg/L) E. coli NHCl 2 (mg/L) PhiX174

10 –2 Adenovirus 3 10 0

E. coli ATCC11229

10 –3 10 –1
10 –1 10 0 10 1 10 2 10 0 10 1 10 2 10 3
(a) Time (min) (b) Time (min)
FIGURE 19.3 Plots of concentration time data for 99% inactivation of microorganisms shown to illustrate Ct concept. (a) HOCl at 08C–68C.
(Adapted from ASCE-WPCF, Disinfection, in Wastewater Treatment Plant Design, Manual of Practice No. 8, ASCE, New York, 1977,
Chapter 20.) (b) Dichloramine: pH ¼ 4.5 and T ¼ 158C. (From Doull, J., Drinking Water and Health, Vol. 2, National Academy Press,
Washington, DC, 1980, p. 28.)