Page 867 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

822 Appendix E: Porous Media Hydraulics

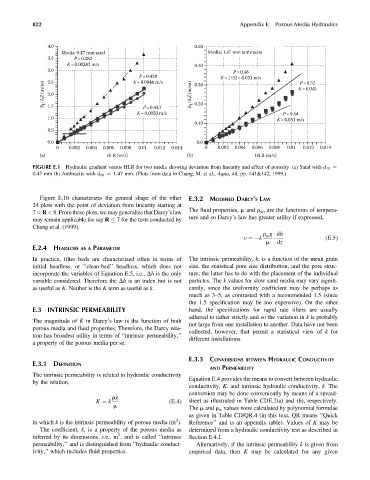
4.0 0.50
Media: 0.47 mm sand Media: 1.47 mm anthracite
3.5 P = 0.382
K = 0.00282 m/s 0.40
3.0 P= 0.48
P= 0.428 0.30 K = 1/32 = 0.031 m/s P=0.52
2.5
K= 0.0046 m/s
h L /ΔZ (m/m) 2.0 h L /ΔZ (m/m) 0.20 K = 0.045

1.5
P= 0.433
K= 0.0050 m/s P=0.54
1.0 K= 0.051 m/s
0.10
0.5

0.0 0.0
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0 0.002 0.004 0.006 0.008 0.01 0.012 0.014
(a) HLR (m/s) (b) HLR (m/s)

FIGURE E.1 Hydraulic gradient versus HLR for two media showing deviation from linearity and effect of porosity. (a) Sand with d 10 ¼
0.47 mm (b) Anthracite with d 10 ¼ 1.47 mm. (Plots from data in Chang, M. et al., Aqua, 48, pp. 141&142, 1999.)

Figure E.1b characterizes the general shape of the other E.3.2 MODIFIED DARCY’S LAW
24 plots with the point of deviation from linearity starting at
The fluid properties, m and r w , are the functions of tempera-
7 < R < 8. From these plots, we may generalize that Darcy’slaw
ture and so Darcy’s law has greater utility if expressed,
may remain applicable for say R 7 for the tests conducted by
Chang et al. (1999).
r g dh
w
v ¼ k (E:5)
m dz
E.2.4 HEADLOSS AS A PARAMETER
In practice, filter beds are characterized often in terms of The intrinsic permeability, k, is a function of the mean grain
initial headloss, or ‘‘clean-bed’’ headloss, which does not size, the statistical pore size distribution, and the pore struc-
incorporate the variables of Equation E.5, i.e., Dh is the only ture; the latter has to do with the placement of the individual
variable considered. Therefore the Dh is an index but is not particles. The k values for slow sand media may vary signifi-
as useful as K. Neither is the K term as useful as k. cantly, since the uniformity coefficient may be perhaps as
much as 3–5, as contrasted with a recommended 1.5 (since
the 1.5 specification may be too expensive). On the other
E.3 INTRINSIC PERMEABILITY hand, the specifications for rapid rate filters are usually
adhered to rather strictly and so the variation in k is probably
The magnitude of K in Darcy’s law is the function of both
not large from one installation to another. Data have not been
porous media and fluid properties. Therefore, the Darcy rela-
collected, however, that permit a statistical view of k for
tion has broadest utility in terms of ‘‘intrinsic permeability,’’
different installations.
a property of the porous media per se.
E.3.3 CONVERSIONS BETWEEN HYDRAULIC CONDUCTIVITY
E.3.1 DEFINITION
AND PERMEABILITY
The intrinsic permeability is related to hydraulic conductivity
Equation E.4 provides the means to convert between hydraulic
by the relation,
conductivity, K, and intrinsic hydraulic conductivity, k. The
conversion may be done conveniently by means of a spread-
rg
K ¼ k (E:4) sheet as illustrated in Table CDE.2(a) and (b), respectively.
m
The m and r w values were calculated by polynomial formulae
as given in Table CD/QR.4 (in this text, QR means ‘‘Quick
2
in which k is the intrinsic permeability of porous media (m ). Reference’’ and is an appendix table). Values of K may be
The coefficient, k, is a property of the porous media as determined from a hydraulic conductivity test as described in
2
inferred by its dimensions, i.e., m , and is called ‘‘intrinsic Section E.4.1.
permeability,’’ and is distinguished from ‘‘hydraulic conduct- Alternatively, if the intrinsic permeability k is given from
ivity,’’ which includes fluid properties. empirical data, then K may be calculated for any given