Page 237 - gas transport in porous media

Chapter 13: Lattice Boltzmann Method
233
bounce-back, this fluid does not experience the free-fluid collision step, and appears
to have a lateral diffusion coefficient of zero.Again, tests suggest the overall error (for
measured vs. theoretical dispersion coefficients) is small, even for narrow channels
(Stockman et al., 1998). Obviously, the effect of the fluid at the interface decreases
as the system is scaled to use more nodes to represent the same solid.
13.4.2 Error in Permeability for Small Channels

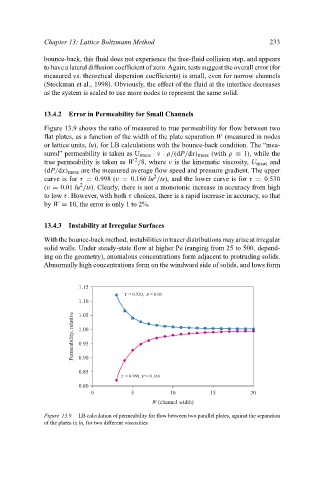
Figure 13.9 shows the ratio of measured to true permeability for flow between two
flat plates, as a function of the width of the plate separation W (measured in nodes
or lattice units, lu), for LB calculations with the bounce-back condition. The “mea-
sured” permeability is taken as U meas · ν · ρ/(dP/dx) meas (with ρ ≡ 1), while the
2
true permeability is taken as W /8, where ν is the kinematic viscosity, U meas and
(dP/dx) meas are the measured average flow speed and pressure gradient. The upper
2
curve is for τ = 0.998 (ν = 0.166 lu /ts), and the lower curve is for τ = 0.530
2
(ν = 0.01 lu /ts). Clearly, there is not a monotonic increase in accuracy from high
to low τ. However, with both τ choices, there is a rapid increase in accuracy, so that
by W = 10, the error is only 1 to 2%.

13.4.3 Instability at Irregular Surfaces
Withthebounce-backmethod, instabilitiesintracerdistributionsmayariseatirregular
solid walls. Under steady-state flow at higher Pe (ranging from 25 to 500, depend-
ing on the geometry), anomalous concentrations form adjacent to protruding solids.
Abnormally high concentrations form on the windward side of solids, and lows form

1.15
t = 0.530, n = 0.01
1.10

Permeability, relative 1.00
1.05

0.95
0.90

0.85
t = 0.998, n = 0.166
0.80
0 5 10 15 20
W (channel width)
Figure 13.9. LB calculation of permeability for flow between two parallel plates, against the separation
of the plates in lu, for two different viscosities