Page 234 - gas transport in porous media

230
10000
Gunn & Pryce sphere Sc = 0.88 Stockman
Koch et al. sphere Sc ~ ∞
Eidsath et al. cylinder Sc ~ ∞
1000 LB sphere Sc = 0.88
LB sphere Sc = 32
LB cylinder Sc = 32
D*/D m 100
10

1

0.1
1 10 100
Pe
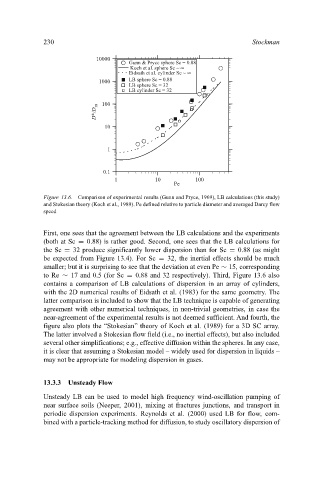
Figure 13.6. Comparison of experimental results (Gunn and Pryce, 1969), LB calculations (this study)
and Stokesian theory (Koch et al., 1989). Pe defined relative to particle diameter and averaged Darcy flow
speed

First, one sees that the agreement between the LB calculations and the experiments
(both at Sc = 0.88) is rather good. Second, one sees that the LB calculations for
the Sc = 32 produce significantly lower dispersion than for Sc = 0.88 (as might
be expected from Figure 13.4). For Sc = 32, the inertial effects should be much
smaller; but it is surprising to see that the deviation at even Pe ∼ 15, corresponding
to Re ∼ 17 and 0.5 (for Sc = 0.88 and 32 respectively). Third, Figure 13.6 also
contains a comparison of LB calculations of dispersion in an array of cylinders,
with the 2D numerical results of Eidsath et al. (1983) for the same geometry. The
latter comparison is included to show that the LB technique is capable of generating
agreement with other numerical techniques, in non-trivial geometries, in case the
near-agreement of the experimental results is not deemed sufficient. And fourth, the
figure also plots the “Stokesian” theory of Koch et al. (1989) for a 3D SC array.
The latter involved a Stokesian flow field (i.e., no inertial effects), but also included
several other simplifications; e.g., effective diffusion within the spheres. In any case,
it is clear that assuming a Stokesian model – widely used for dispersion in liquids –
may not be appropriate for modeling dispersion in gases.

13.3.3 Unsteady Flow
Unsteady LB can be used to model high frequency wind-oscillation pumping of
near surface soils (Neeper, 2001), mixing at fractures junctions, and transport in
periodic dispersion experiments. Reynolds et al. (2000) used LB for flow, com-
bined with a particle-tracking method for diffusion, to study oscillatory dispersion of