Page 219 - Geochemical Anomaly and Mineral Prospectivity Mapping in GIS

Knowledge-Driven Modeling of Mineral Prospectivity 221

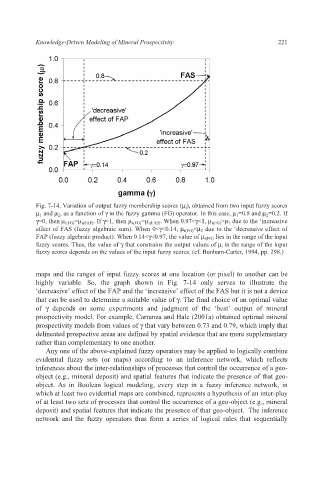
Fig. 7-14. Variation of output fuzzy membership scores (μ i ), obtained from two input fuzzy scores
μ 1 and μ 2 , as a function of γ in the fuzzy gamma (FG) operator. In this case, μ 1 =0.8 and μ 2 =0.2. If
γ=0, then μ i(FG) =μ i(FAP) . If γ=1, then μ i(FG) =μ i(FAS) . When 0.97<γ<1, μ i(FG) >μ 1 due to the ‘increasive
effect of FAS (fuzzy algebraic sum). When 0<γ<0.14, μ i(FG) <μ 2 due to the ‘decreasive effect of
FAP (fuzzy algebraic product). When 0.14<γ<0.97, the value of μ i(FG) lies in the range of the input
fuzzy scores. Thus, the value of γ that constrains the output values of μ i in the range of the input
fuzzy scores depends on the values of the input fuzzy scores. (cf. Bonham-Carter, 1994, pp. 298.)

maps and the ranges of input fuzzy scores at one location (or pixel) to another can be
highly variable. So, the graph shown in Fig. 7-14 only serves to illustrate the
‘decreasive’ effect of the FAP and the ‘increasive’ effect of the FAS but it is not a device
that can be used to determine a suitable value of γ. The final choice of an optimal value
of γ depends on some experiments and judgment of the ‘best’ output of mineral
prospectivity model. For example, Carranza and Hale (2001a) obtained optimal mineral
prospectivity models from values of γ that vary between 0.73 and 0.79, which imply that
delineated prospective areas are defined by spatial evidence that are more supplementary
rather than complementary to one another.
Any one of the above-explained fuzzy operators may be applied to logically combine
evidential fuzzy sets (or maps) according to an inference network, which reflects
inferences about the inter-relationships of processes that control the occurrence of a geo-
object (e.g., mineral deposit) and spatial features that indicate the presence of that geo-
object. As in Boolean logical modeling, every step in a fuzzy inference network, in
which at least two evidential maps are combined, represents a hypothesis of an inter-play
of at least two sets of processes that control the occurrence of a geo-object (e.g., mineral
deposit) and spatial features that indicate the presence of that geo-object. The inference
network and the fuzzy operators thus form a series of logical rules that sequentially